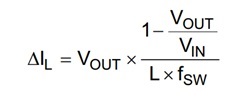Power-supply designers have used various forms of Equation 1 for decades in order to select the correct inductance for their step-down (buck) converters. While Equation 1 is still correct, why should you use it in low-power step-down converter designs?
Typically, Equation 1 swaps the inductance, L, and the inductor ripple current, ΔIL, in order to solve for L based on a given ΔIL. ΔIL is usually set between 20% and 40% of the full load current. This enables designers to easily calculate the required inductance, simplifying a major piece of their design. But why is the ripple current set between 20% and 40%? There is no clear consensus as to whether 20% to 40% is the right range to use. But there are several possible reasons for setting the ripple current this way:
- Since the boundary of discontinuous conduction mode (DCM) and continuous conduction mode (CCM) is at load currents that are one-half the ripple current, 20-40% ripple gives a DCM/CCM boundary at a 10-20% load current. Older power supplies may have had a minimum load at this level, which would allow the power supply to operate in CCM only. Thus, the waveforms, behavior and calculations needed would just be for one operating mode instead of two.
- In high-current power supplies, 20-40% ripple gives reasonable levels for peak current limit protection. For example, a 50A power supply with 40% ripple (20A peak to peak) needs the peak current limit set at or above 60A (50A plus one-half of 20A) to not trip at load currents below 50A. If the ripple is set at 100%, this level would need to be at least 75A.
- If the output capacitor is either tantalum or electrolytic, the inductor ripple current multiplied by the capacitor’s equivalent series resistance (ESR) defines the output voltage ripple. Lower current ripple is necessary to achieve lower voltage ripple. There are also reliability limits on the allowable ripple current in the capacitors themselves.
But in low-power step-down converters, none of these reasons are particularly valid. Why?
- The minimum loads can be quite low – very often in the microampere or milliampere range. This makes designing for CCM-only operation impossible (for asynchronous converters) or very inefficient (for synchronous converters).
- Lower power means that the current-limit set-point difference is usually either ~3A (for 20-40% ripple) or ~4A (for 100% ripple). There is not as significant a jump with the increase in current ripple.
- The smaller size of low-power converters necessitates a higher switching frequency. Combined with advances in ceramic-capacitor technology, there is rarely significant ESR in the output capacitance. Instead, a small amount of ceramic capacitance can reliably handle larger ripple currents while delivering very-low-output voltage ripple.
In addition, most low-power converters such as the TPS62130A have internal control-loop compensation. This requires selecting the inductance to match the compensation for stability. You cannot select the inductance first and then design the compensation to match it, as with other converters.
So why should you use Equation 1 in low-power step-down converters? There are generally two main reasons: to identify the DCM/CCM boundary and to determine the peak inductor current. The DCM/CCM boundary is also the power-save mode (PSM)/pulse width modulation (PWM) mode boundary for DCS-Control devices, while the peak inductor current is needed to appropriately size the inductor current rating and to verify that the design will not trip the internally set current limit.
Rather than start with Equation 1 and select an inductance, a TPS62xxx device gives recommended inductors/inductances from which to choose. You can either pick one from the list or complete the calculations yourself to check if a different inductor will work in your specific design.
Why might inductor ripple current as a percentage still be relevant for your designs?