This technical article was updated on July 23, 2020.
In talking to system designers using analog-to-digital converters (ADCs), one of the most common questions that I hear is:
“Is your 16-bit ADC also 16-bit accurate?”
The answer to this question lies in the fundamental understanding of the difference between the concept of resolution and accuracy. Despite being two completely different concepts, these two terms are often confused and used interchangeably.
Today’s blog post details the differences between these two concepts. We will dig into the major contributors of ADC inaccuracy in a series of posts.
The resolution of an ADC is defined as the smallest change in the value of an input signal that changes the value of the digital output by one count. For an ideal ADC, the transfer function is a staircase with step width equal to the resolution. However, with higher resolution systems (≥16 bits), the transfer function’s response will have a larger deviation from the ideal response. This is because the noise contributed by the ADC, as well as driver circuitry, can eclipse the resolution of the ADC.
Furthermore, if a DC voltage is applied to the inputs of an ideal ADC and multiple conversions are performed, the digital output should always be the same code (represented by the black dot in Figure 1). In reality, the output codes are distributed over multiple codes (the cluster of red dots seen below), depending on the total system noise (i.e. including the voltage reference and the driver circuitry). The more noise in the system, the wider the cluster of data points is and vice-versa. An example is shown in Figure 1 for mid-scale DC input. This cluster of output points on the ADC transfer function is commonly represented as a DC histogram in ADC datasheets.
Figure 1: Illustration of ADC resolution and effective resolution on an ADC transfer curve
The illustration in Figure 1 brings up an interesting question. If the same analog input can result in multiple digital outputs, then does the definition of ADC resolution still hold true? Yes, it does if we only consider the quantization noise of the ADC. However, when we account for all the noise and distortion in the signal chain, the effective noise-free resolution of the ADC is determined by the output code-spread (NPP), as indicated in equation (1).
In typical ADC datasheets, the effective number of bits (ENOB) is specified indirectly by the AC parameter and signal-to-noise and distortion ratio (SINAD), which can be calculated by equation 2:
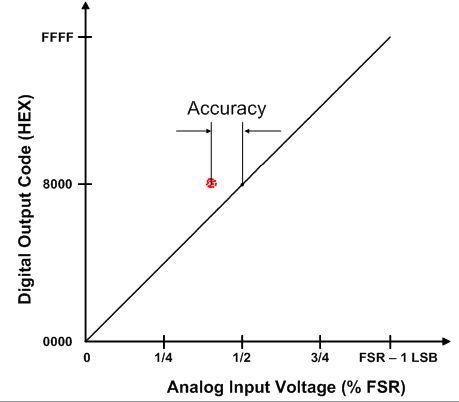
Next, consider if the cluster of output codes (the red dots) in Figure 1 was not centered on the ideal output code and was located somewhere else on the ADC transfer curve away from the black dot (as represented in Figure 2). This distance is an indicator of the data acquisition system’s accuracy. Not only the ADC but also the front-end driving circuit, reference and reference buffers are all contributors to the overall system accuracy.
Figure 2: Illustration of accuracy on ADC transfer curve
The important point to be noted, the ADC accuracy and resolution are two different parameters that may not be equal to each other. From a system design perspective, accuracy determines the overall error budgeting of the system, whereas the system software algorithm integrity, control and monitoring capability depend on the resolution.
In my next post, I’ll talk about key factors that determine the “total” accuracy of data acquisition systems.
Related posts on the hub:
- SAR ADC performance considerations and other SAR ADC-related posts
- Accurate data acquisition