Continued from Part 1 of my blog series on quantifying harmonic distortion.
As a less computationally intensive alternative to calculating each harmonic RMS value for THD, you can estimate THD by calculating the total RMS of the harmonics (excluding the fundamental). First, calculate the RMS of the fundamental and subtract it from the total RMS. Equations 1 through 4 are the resulting THD representations:
The Total Harmonic Distortion Measurement for Energy Monitoring Reference Design (TIDM-THREADING) uses this method of calculating THD to add THD calculations to the Class 0.2 accuracy, three-phase EVM430-F6779 evaluation module (EVM). In this EVM, a MSP430F67791A e-meter system-on-chip (SOC) drives the LCD and keeps track of the time, as well as senses and calculates metrology parameters. The MSP430F67791A has internal delta-sigma converters that are used to sense each voltage and each current. This particular design must use current transformers as the current sensors to ensure the necessary isolation when interfacing to the different line voltages of a three-phase system. Additionally, the design uses a sample rate of 4,096 samples per second and calculates the following phase-metrology parameters: RMS voltage, RMS current, RMS active power, reactive power, apparent power, line frequency, power factor, phase-to-phase angle, voltage sag and swell, fundamental voltage, fundamental current, fundamental active power, and fundamental reactive power.
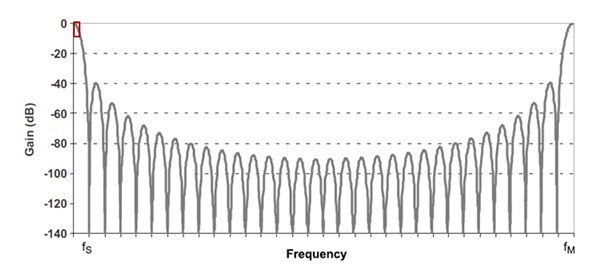
In this reference design, the delta-sigma converters ensure accurate active power readings; however, one disadvantage is that the frequency response of the converter’s sinc3 digital filters causes attenuation of the harmonic amplitudes. Figure 1 shows the sinc3 filter frequency response for an oversampling ratio (OSR) of 32. Note that this application does not use an OSR = 32 shown in Figure 1; the reference design uses an OSR of 256. However, Figure 1 clearly shows an example frequency response of the sigma-delta converters.
Figure 1: Sinc3 Frequency Response for an Oversampling Ratio of 32
In Figure 1, the portion of the frequency response shown in the red box at the upper-left corner is an example of the frequency ranges of interest for harmonic analysis. The maximum frequency that can be sensed is half the sampling frequency (fs/2). In this red box, notice how the gain decreases with increasing frequency. This causes the attenuation of harmonics at higher frequencies, which in turn induces error in the calculation of THD and total RMS. The current transformer(CT) current sensors are another source of error when performing power-quality analysis, because they cause variable phase shifts across frequency.
For many e-meters, you may need only a rough estimate for THD. In such systems, minimizing cost may be one of the driving factors for your design. In such cases, the Total Harmonic Distortion Measurement for Energy Monitoring Reference Design will be a good fit.
But what about systems that require more accuracy for THD measurements and metrology parameters in the presence of harmonics? In the next installment of this series, I will talk about another reference design – a poly-phase shunt system that prevents the degradation of power-quality results from using CTs, while employing an architecture that reduces the attenuation of higher-frequency harmonic components from the sinc3 filter.
Additional resources:
- Read Quantifying harmonic distortion: Options for calculating THD.
- Learn about power quality in the following blog, "Power quality is essential to a smarter grid."
- Download the following reference designs related to THD: