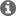Other Parts Discussed in Thread: TINA-TI, THS4131, OPA1632
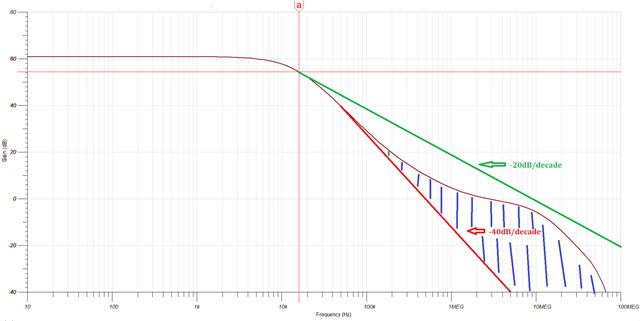
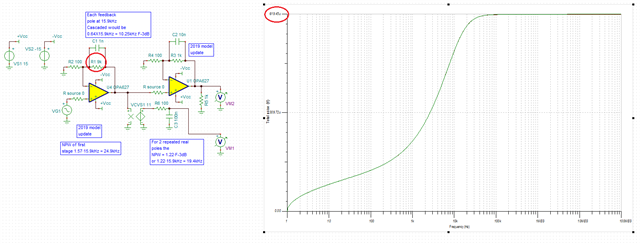
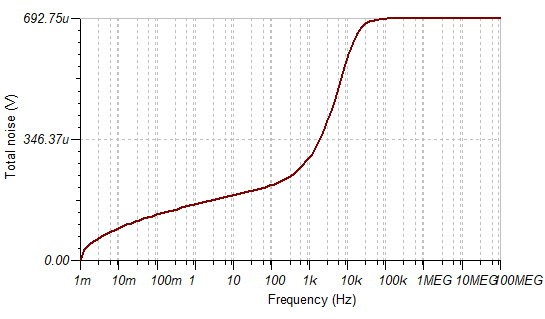
Hi there, I am watching TIPL video section 8.4. on page 15 of the slide, when add LPF capacitors, I thinks the Noise BandWidth shoud use Kn=1.22 (rather than 1.57) for U1.
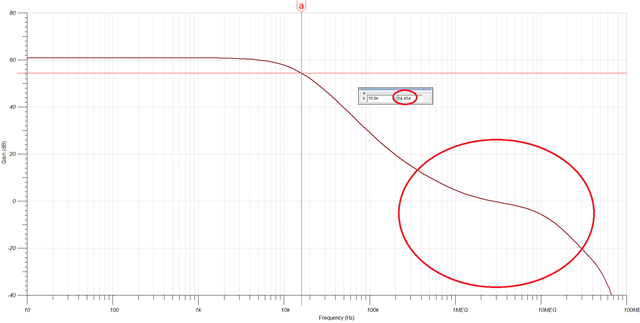
Yes, the noise gain of U2 can be ignored by the simplifying rules, but the Low Pass Filter of U2 (C2 and R4) still workhere. Since f1=f2, I think it should be a -6dB (2nd order) filter for noise on U1's positive input.
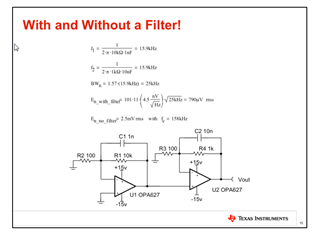
Did I misunderstand something?
Further more, a more general question will come out, if U1 and U2 use very different cut-off frequencies, different orders, and even different topology, how should we determin the order of the filter ?
Thanks!