Other Parts Discussed in Thread: OPA210
Hi,
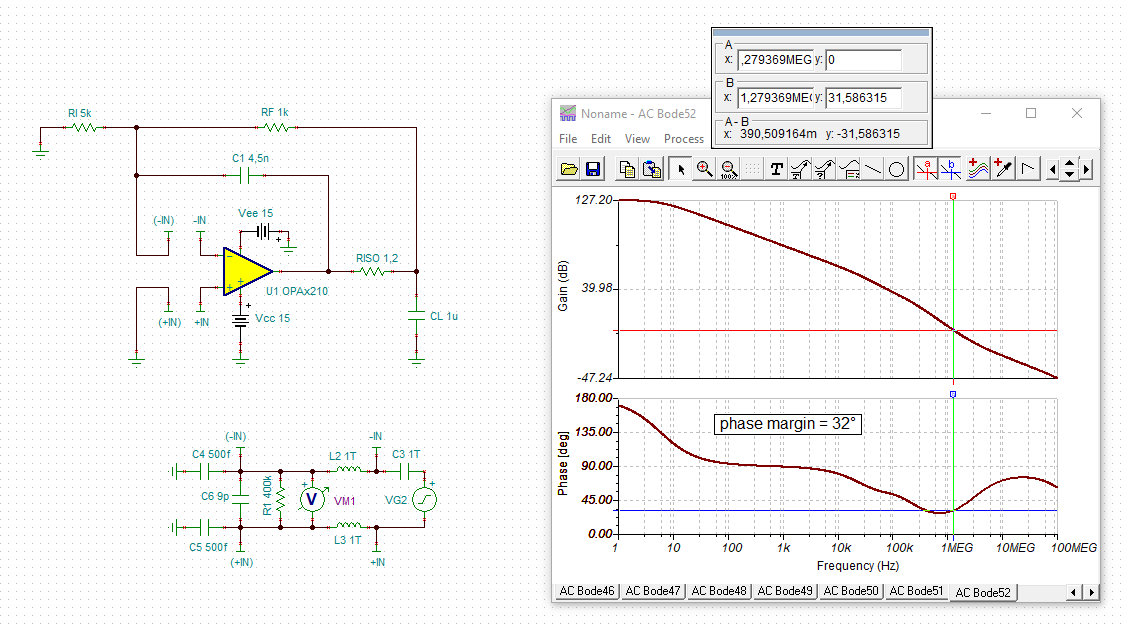
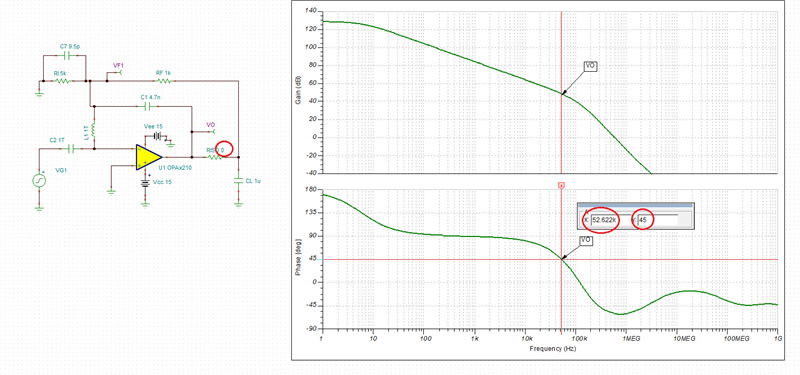
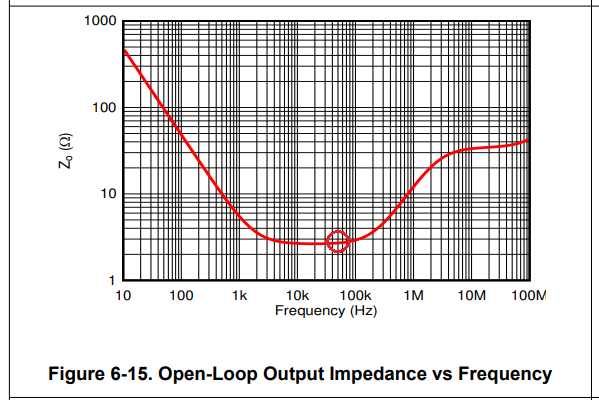
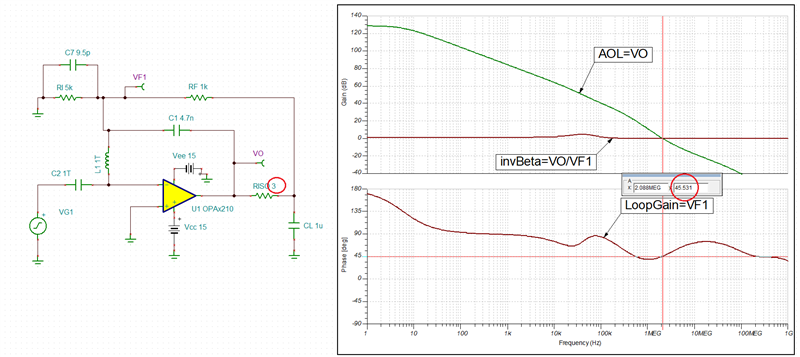
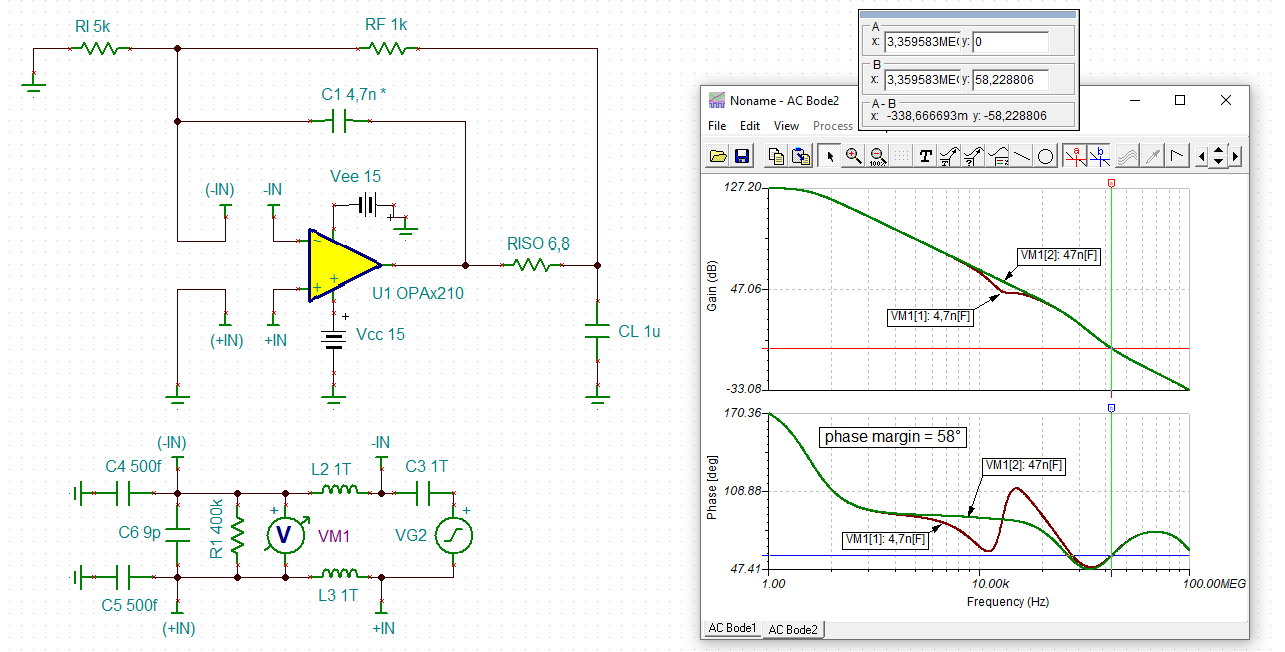
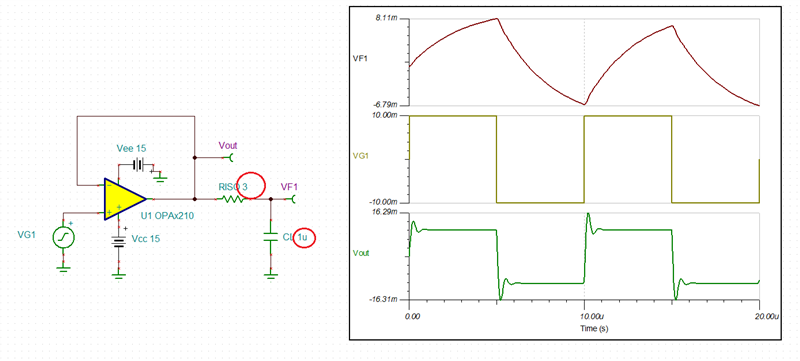
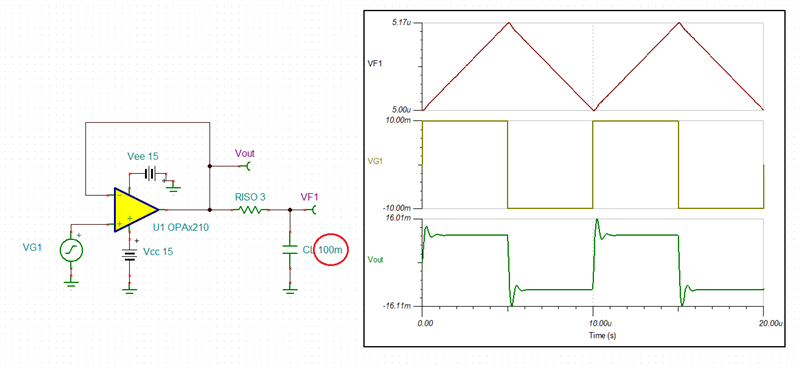
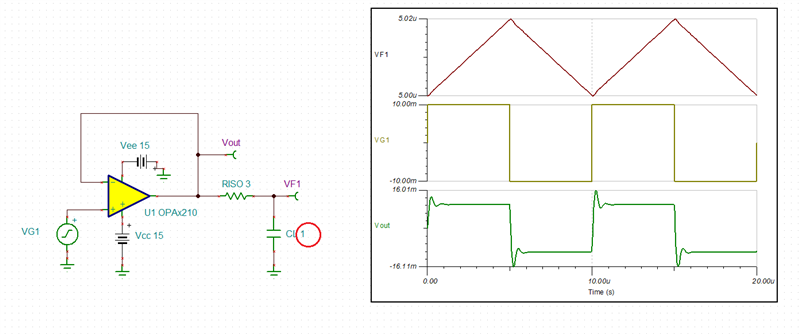
I need to simulate the stability for OPA2210. I download the TINA model from TI website. And I have done a TINA simulation. But I am not sure CF and RISO value is correct.
OPA2210 input common capacitance is 0.5pF, and the input differential capacitance is 9pF. so the input total capacitance is 9.5pF.
RF=1K, RI=5K.
Could you help me to check the TINA simulation and send me a correct OPA2210 TINA simulation for the stability?