Hello,
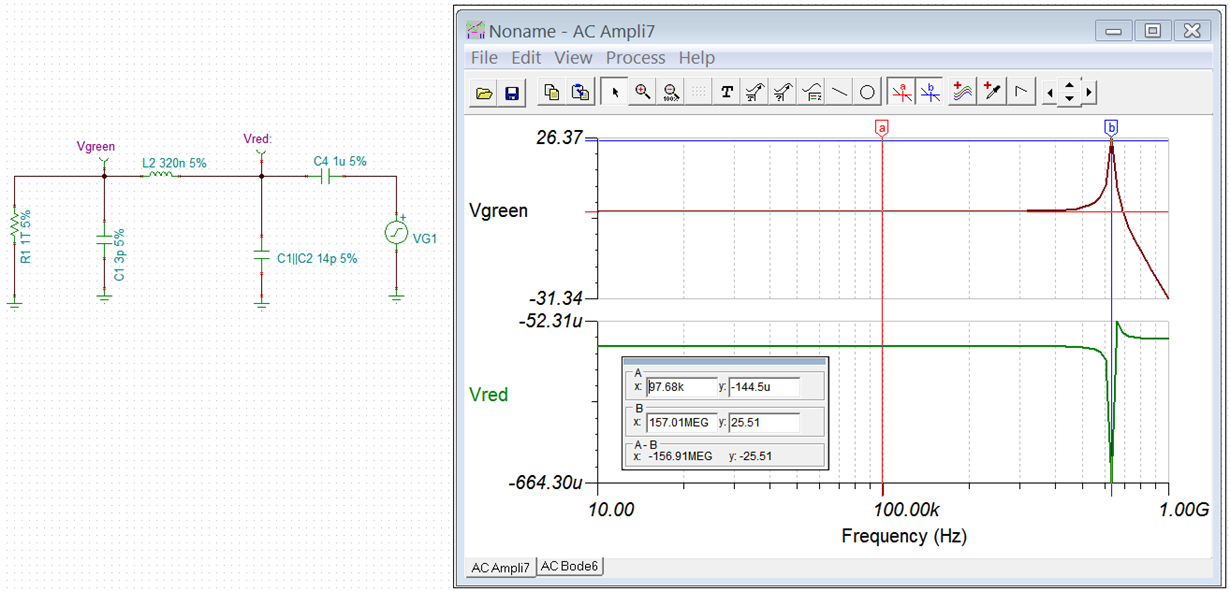
Simulating this simplest case (please, see schematic in attached pdf), I've got this starnge waveform:
How this non-linear shape resulted out from linear schematic ?
Thanks,
Sincerely,
Pavel.
P.S. Additional question: how specify internal resistance of voltage source ?