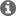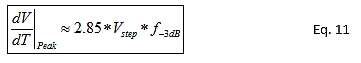Other Parts Discussed in Thread: LMP7718, OPA837
Hi,
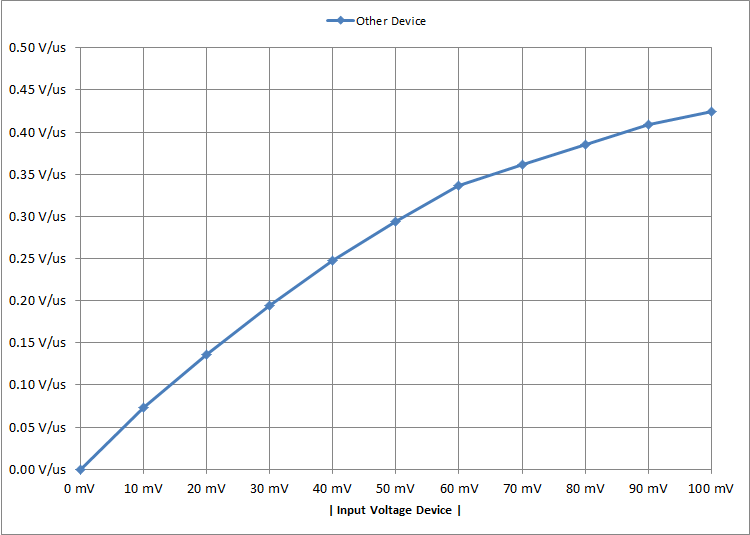
The slew rate of TLV6742 is lower than customer's requirements, however the input signal of customer's system is 2mV, which is small-signal. And from the precision lab training, the rise time of a small-signal step input is based on the op-amp’ s bandwidth and the rise time does not match up with the slew rate spec.
Questions:
1. For customer's system:
f_c=GBW/G_cl =10MHz/48=208kHz
t_r=0.35/f_c =0.35/294kHz=1.68μs (Rise time)
Does it mean that no matter how much is the output voltage, the rise time is equal to 1.68μs? But our customer requires the output to get to 3.3V within 1μs. Is the rise time in conflict with the requirement?
2. If the rise time does not match up with the slew rate spec, does it mean that i can choose an amp with arbitrary slew rate?
I'm confused by the rise time and the slew rate, and I really look forward to your reply.
Backup information:
Best regards,
Wendy