Hi,
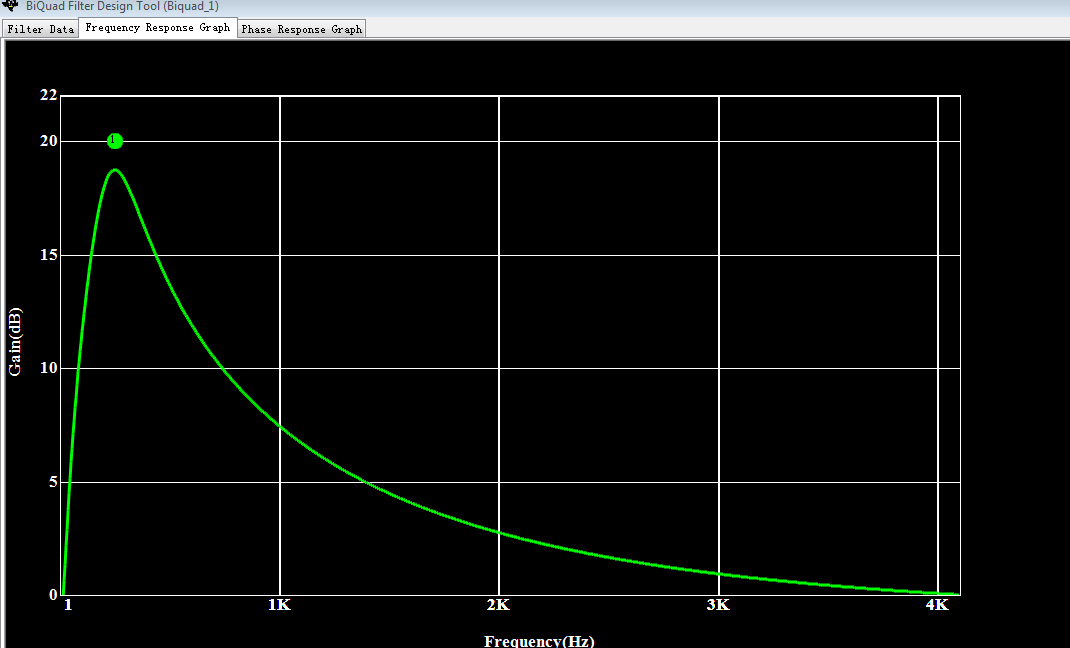
I want to use the Biquad Filter Design Tool in the PurePath Studio. I choosed Equalizer(Q factor) and other factors as shown in Fig.1. And then it produced a frequency responce graph as shown in Fig.2. I wan to know the functional relationship about the X-axis(frequency) and Y-axis(Gain) . Is there someways?
Best regards!
Maolin. Shi
Fig.1
Fig.2