Hello,
I'm working on a project with the AMC1210. At the input from the AMC1210 I apply the signals from the AMC1203 (MCLK and MDAT). I provide a differential voltage of 110mV at the input of the AMC1203. Now I configure the AMC1210 so that it runs with a sinc1 or sinc2 filter and experimenting with the oversampling ratios of the sinc filter unit. I don't modify any other register because I only want to get back the the 110mV that I provided at the input of the AMC1203. I've chosen the 16-bit data representation and communicate via SPI to the AMC1210. Now is my question: how can I find back the 110mV from the data that I'm reading from the AMC1210?
I did some measurements and these are the results:

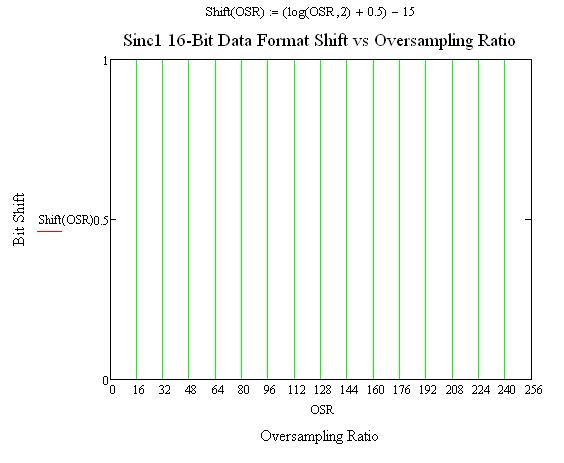
Sinc1 data:

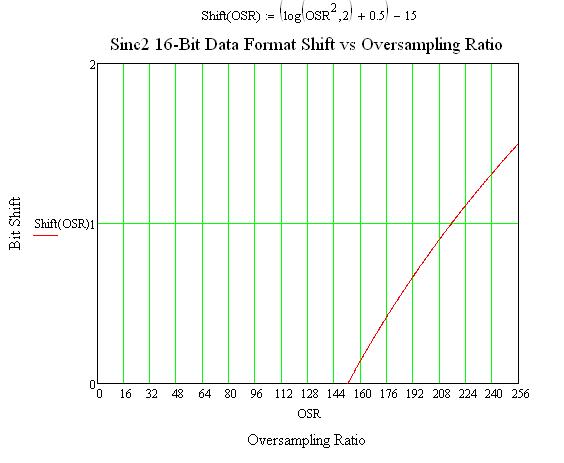
Sinc2 data:

Thanks in advance!
Mathieu