Other Parts Discussed in Thread: ADS1018, ADS1605
hi team
Customer would like to calculate TUE for ADS1018-Q1,
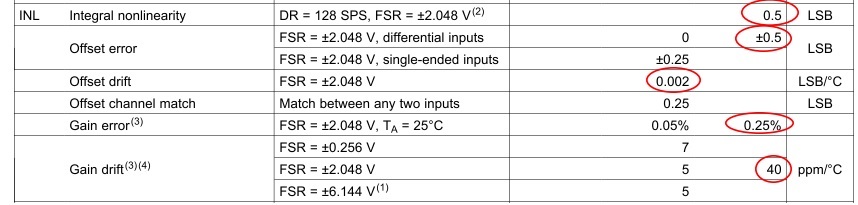
but D/S has only information for FSR = +- 2.048V as below.
the following TUE calculated is OK for FSR = +- 6.144V case ?
FSR = ±6.144V,
Resolution = FSR x 2 / 2^bits = 6.144V x 2 / 2^12 = 3[mV]
Max Offset =0.5[LSB],
Max Offset drift over temperature = 0.002 [LSB/⁰C] x (125⁰C - 25⁰C) = 0.2[LSB]
MAX INL = 0.5[LSB],
Max DNL = 0[LSB],
Max GainError = 0.25[%]/100 x FSR x 2 / Resolution = 0.25[%]/100 x 6.144V x 2 / 3[mV] = 10.24[LSB]
Max Gain Drift over temperature = 40[PPM/⁰C]/10000 x (125⁰C - 25⁰C) x FSR x 2 /Resolution = 40[PPM/⁰C]/10000 x (125⁰C - 25⁰C)/100 x 6.144V x 2 / 3[mV] = 16.384[LSB]
hence, Max TUE = SQRT[ Vos^2 + INL^2 + DNL^2 + GainError^2 ] = SQRT[(0.5+0.2)^2 + 0.5^2 + 0^2 + (10.24+16.384)^2] = ±26.637[LSB]
Max TUE = 3[mV] x 26.637[LSB] = ±79.91[mV]