Hello,
I would like to have further explanations about SN65LVCP22 2x2 LVDS CrossPoints.
The part will be used in a 2:1 mux architecture.
1. Clarification on the differences between bit rate and frequency
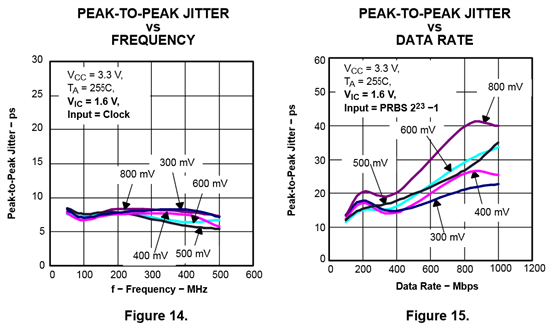
I have seen in the datasheet several charts that depict both the peak-to-peak jitter evolution in function of the frequency and the peak-to-peak jitter evolution depending on the bit rate. Having read those charts I do not understand why the peak-to-peak jitter value given a frequency is different from the peak-to-peak jitter value read for the equivalent bit rate at equal conditions.
What I mean by "equivalent bit rate" is for example a signal at a bitrate of 1000Mbps has its fundamental frequency at 500MHz (is it correct?). Then, continuing with both 500MHz and 1000Mbps values, and reading the peak-to-peak jitter values on the two charts below (referenced as Figures 14 and 15 in the datasheet), for 800mV curb the peak-to-peak jitter is 7ps@500MHz on the Figure 14 and 40ps@1000Mbps on the Figure 15.
Thus my question is: why are the two values different each other while I thought they would be equal?
Did I miss something and what?
The question is applicable to both the charts and the table extracted from the SN65LVCP22 datasheet shown below.
Finally, what value should I take to calculate total jitter?
2.Total jitter calculation
How should I deal with peak-to-peak and random jitter values in order to evaluate a jitter budget?
I have read in literature that: Total_Jitter = Deterministic_Jitter + 2*N*Random_Jitter where N is a factor depending on the BER we would like to reach.
For example:
(1) BER = 1e-16 --> N=8,222 --> TJmax@1000Mbps = 105 + 8,222*1,8 = 120ps
However, the last time I used a LVDS buffer/reapeater similar to the SN65LVCP22, it has been said to me that as the repeater does not lock to any PLL the Total_Jitter has to be simply Deterministic_Jitter + Random_Jitter (without the factor 2*N).
For example:
(2) TJ =105 + 1,8 = 106,8ps
Thus, what is the good calculation (1 or 2 or other) for the SN65LVCP22?
3. Pulse skew
It has also been said to me that pulse skew do not have to be added to DJ and RJ to calculate the budget jitter. However I do not understand why.
I know what is Pulse Skew (that is time difference between Low-to-High and High-to-Low Delay) thus I would think that it has an influence on jitter. But as written above, it has been said to me that pulse skew as no influence on jitter...
I would be really grateful if anyone could explain me if and why Pulse Skew does not need to be added when calculating either the budget jitter or the receiver skew margin.
4. Relation between input and output jitters
Does the SN65LVCP22 do data recovery? As it is only a repeater/buffer I would say it does not.
If it does not do recovery of the data, then: does the output jitter equal jitter received to the input + total jitter that the SN65LVCP induces ?
Let's have an example: assuming an input jitter of 180ps (whatever the frequency or the bitrate of the signal received), the SN65LVCP22 adds the jitter calculated in 2 - example (1) that is 120ps, then the total output jitter is 180 + 120 = 300ps.
Is it the good way for calculating the jitter to the output?
Thank for responding
Julien Appaix