MSP430FR5994: LEARAM question

user6140878

Part Number: MSP430FR5994
Other Parts Discussed in Thread: TIDM-FILTERING-SIGNALPROCESSING, MSP-EXP430FR5994

Hi,

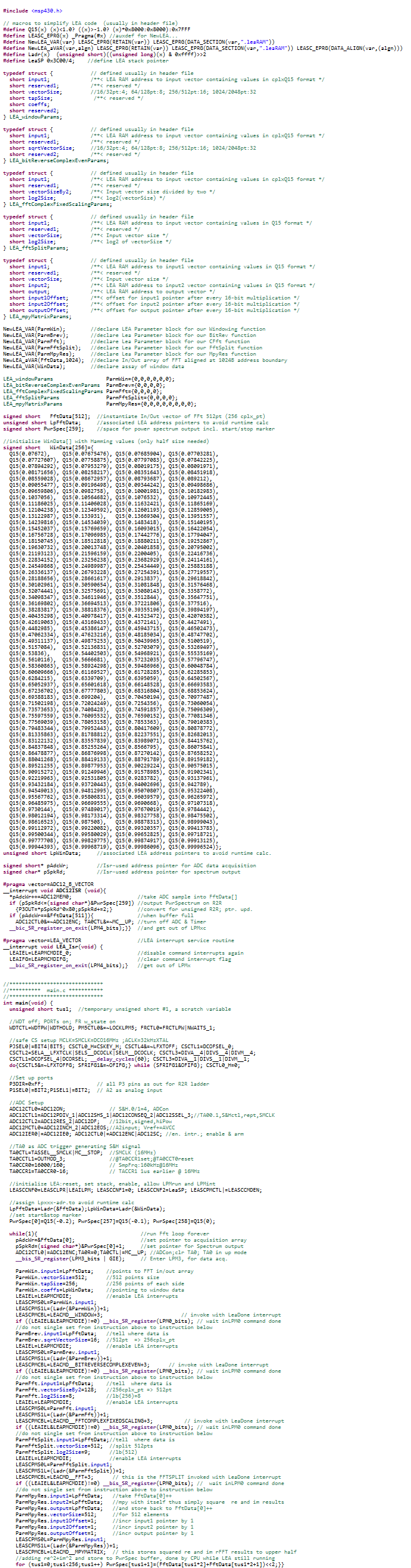
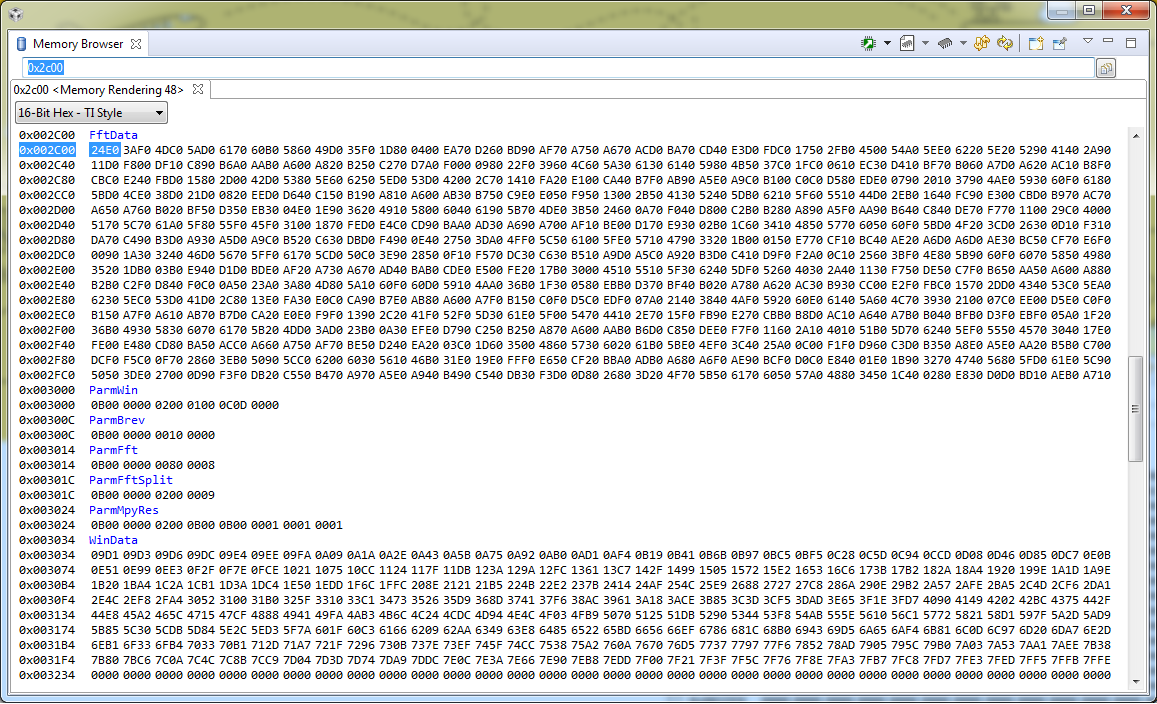
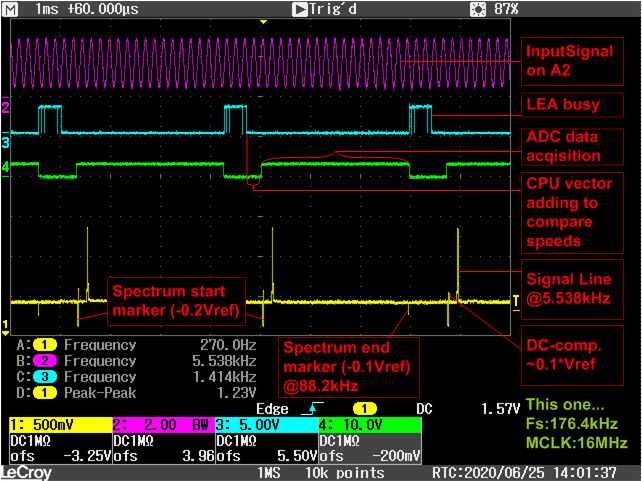
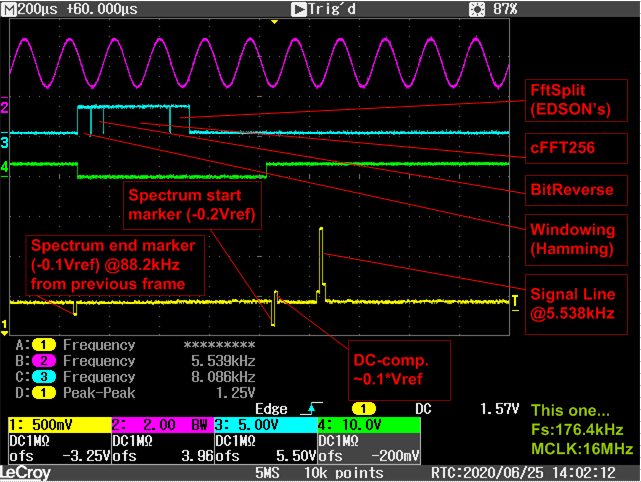
We are testing FFT with LEA with the sample codes from the TI design
"TIDM-FILTERING-SIGNALPROCESSING"

This sample code is designed for "256-point complex FFT" but we need 512-point.

In this sample code define LEARAM
struct FftData_s
{
_q15 input[VECTOR_SIZE*2];
_q15 samples[VECTOR_SIZE*2];
_q15 hamming[VECTOR_SIZE];
} fftDataParam;
When VECTOR_SIZE= 256.this structure need RAM: 2560bytes
we need 512-point complex FFT, so define VECTOR_SIZE = 512
we define 1 channel AD sample
struct FftData_s
{
_q15 input[VECTOR_SIZE*2];
_q15 samples[VECTOR_SIZE];
_q15 hamming[VECTOR_SIZE];
} fftDataParam;
if VECTOR_SIZE = 512,the structure need 4096bytes,But it's beyond the limit of LEARAM(-Z(DATA)LEARAM=2C00-3AC7).
Could you please let us know how to solve this question?
Don't we use the Hamming window to reduce the length of LEARAM?

over 3 years ago

0 Johann Zipperer over 3 years ago

TI__Intellectual 2100 points

Hi Jiangsu,

LEA got the additional functions to generate Real valued FFTs from complex valued ones.

Therefore you can have 256pt_cFFT with memory requirement re-16bit, im-16bit => 1pt=4bytes thus 256pt_cFFT requires 1kb since we do an in place transformation (input vector gets destroyed). This vector needs to start at an 1kb aligned address those could be the addresses 0x2c00; 0x3000, 0x3400.

You now can use the Edson's algorithm to split the complex outputs to twice the points of real spectrum. This would give you the pos. spectrum only therefore the equivalent of 512 pts.

For an true 512pt_cFFT the input_vector=output_vector has to be aligned to 2kb address boundary => this leaves the address 0x3000 as start address. Still the Edson's post processing works there as well. For 512pts I recommend auto scaling to maintain highest accuracy. 512bits on fix scaling loose up to 9 bits; on auto scaling 4-5 bits.

that much for now.

let me know what you want to do

Johann

0 user6140878 over 3 years ago in reply to Johann Zipperer

Prodigy 30 points

Hi Johann
Thank you very much for your quick response
we want to make a design: we need 1-ADC signal sample, to do 512points complex FFT.
just like you say,"the input_vector=output_vector has to be aligned to 2kb address boundary"
then 512point ADC samples needs 1kb，2kb + 1kb = 3kb,now we want to use hamming-windows,512pts hamming windows need 1kb?ok?
but the LEARAM must less than 4kb length,
so can you help me, give me an example or some suggest, for a 512points comlex FFT ,How to define these LEARAM variables?

Best regards

Fei

0 Johann Zipperer over 3 years ago in reply to user6140878

TI__Intellectual 2100 points

Hello again.

sorry for the delay, but we had public holiday yesterday....

The total memory requirement is... (simple approach; blockwise acquisition, then 512pt cFFT, then block post processing)

Vector1 (512 entries 16bit cmplx = 2048bytes ) aligned on 2k address bundary

Vector2 (256 entries 16bit real =512bytes) holding symmetric real valued hamming table; half of it

MSP430 actions

1. ADC data acquisition to real parts of V1re; this are 512 values

2. zero the imaginary part of V1im; to remove all residues from past

3. multiply V1re*V2=>V1re with incrementing index 256 pts, starting at V1[0],V2[0]=>V1[0] ;hamming in re-part

4. multiply V1re*V2=>V1re with decrementing index of V1 256 pts, starting V1[511],V2[0]=>V1[511] ;hamming on re-part

5. cBREVx function from V1=>V1; this reorders the samples to get a linear ordered output

6. cFFT function from V1=>V1; this does the complex FFT

--- the results of the spectrum is in V1re,im as complex number V1[0] is holding the DC value

7. {optional} V1*V1=>V1; all 512pt on real and complex ; this is the first part of the complex absolute / polar transform

8. {optional} V1even+V1odd=>V1 with index V1e:2; V1o:2; =>V1:1 this adds the real and imaginary squares to the

final real vector residing in the lower half of V1. ; this is the 2nd part of the complex absolute.

- done -

Now we re-used the memory vectors again and again to get along. This might not work in all cases, you might want to do a new block or ADC sampling while LEA is chewing on the previous block. On top of that you might want to do additional stuff, like tracking the most dominant frequency in the spectrum... . This requires then that you have alternating vectors and you then just change the pointers to them.

For an true complex 512pt FFT plus Hamming with alternate input vector you would need 4.5kB of LEA-RAM.

Here you can use an MSP430 with 8K LEA-RAM like the 'FR5043.

Alternatively you can use the trick with the symmetry (Edson's algorithm).

The results above (after step 6 ) generates the positive spectrum from V1[0]...V1[255] and a negative spectrum from V1[511]...V1[257]. The values of the positive spectrum and the negative spectrum however are the same since we zeroed out all the imaginary components of our ADC samples in step 2

Filling up the V1 with ADC-samples in an interleaved manner (V1re[0];V1im[0];V1re[1]...V1im[255] )allows you to use the 256pt cFFT for 512 real points and get 256pt as positive spectrum back. Then you need only 1.5kB LEA-RAM for the simple case and 2.5kB LEA-RAM for the continuous case with alternate vectors.

have a nice day

Johann

0 Johann Zipperer over 3 years ago in reply to Johann Zipperer

TI__Intellectual 2100 points

Hello again,

I know it was a bit unfair to talk about how easy and simple it is to save LEA memory and not show by example. Therefore I took some time to code your problem on CCS. Below the solution I would propose. It is a rFFT512 with Hamming, runs with 160kHz sampling frequency from ADC12_A2. The code below runs on an MSP-EXP430FR5994board with R2R ladder to mimic a DAC. CodeSize=1086bytes; Table:695bytes; LEA-Ram:1588bytes. Spectrum data output done on an R2R network on Port3. Speed:235+ complete measurement loops/sec (includes data acq.,rFFT, and spectrum output). Net rFFT time:~460us @16Mhz.

The above code is by far not optimized; I used this style for easier illustration. The ULP-advisor still complains here and there. A complaint-free but less readable variant is given further down.