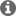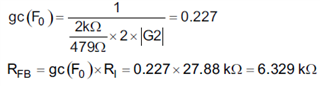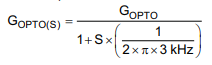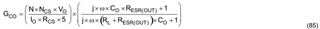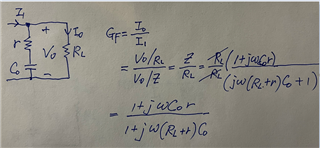Hi Sir,
In the document "Understanding and Designing an Active Clamp Current Mode Controlled
Converter Using the UCC2897A"
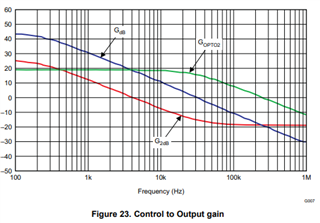
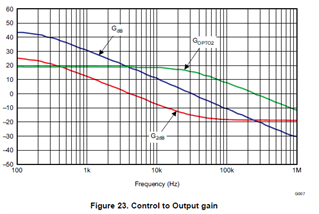
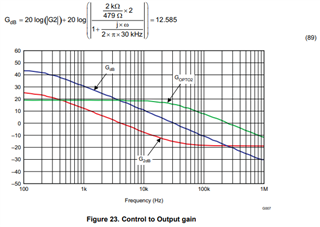
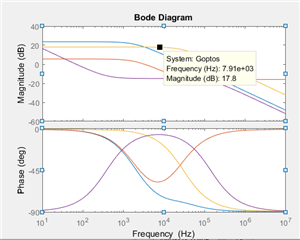
Can any one clarify below equation, how to get 12.5db at 8kHz frequency.

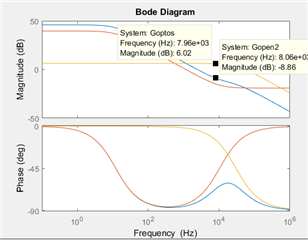
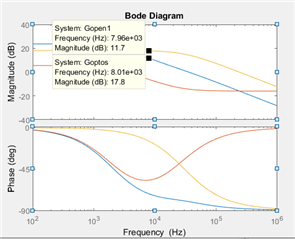
I have considered all the parameters from the document. As per my matlab program, the answer is -6.3db at 8kHz. The code is given below for the reference.
clc
s = tf('s');
Co = 660e-6;
Resr = 10e-3;
Vo =3.3;
Po = 100;
Rload_F = Vo^2/Po;
Rload_10 = Vo^2/(0.1*Po);
Ncs = 100;
N = 6; %22/12;
Rcs = 6.9; %0.347;
Io = Po/Vo;
Vref = 5;
Vfbmax = 2.4; %(0.95*1.27)*(5/2);
Irefmin = 1.3e-3;
Rvref = (Vref-Vfbmax)/Irefmin
% if CTR_min is 100 percentage
Ioptomin = Irefmin;
ITL431 = Ioptomin;
Vopto = 4.5;
Vf = 1.3;
Vsc = 1.24;
Fo = 8e3;
Ropto = ((Vopto-Vf-Vsc)/ITL431)/3
CTR = 2;
Gopto = (Rvref/479)*CTR;
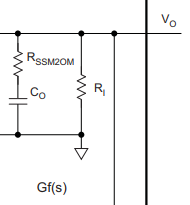
GFs = ((s*Co*Resr*Rload_F)+Rload_F)/((s*(Rload_F+Resr)*Co)+1);
GF_mins = ((s*Co*Resr*Rload_10)+Rload_10)/((s*(Rload_10+Resr)*Co)+1);
K = (N*Ncs*Vo)/(Io*Rcs*(5));
G2db_atFo=20*log10(K)+20*log10((sqrt(((2*pi*Fo*Co*Resr*Rload_10)^2)+((Rload_10)^2))))+20*log10(1/(sqrt((2*pi*Fo*(Rload_10+Resr)*Co)^2+1)))
Goptodb_atFo = 20*log10(Gopto)+20*log10(1/sqrt(1+(2*pi*Fo*(1/(2*pi*30e3)))^2))
Gopen_db = G2db_atFo+Goptodb_atFo
Please clarify if my code have any mistakes.
Thanks and Regards
Umamaheswararao