- Ask a related questionWhat is a related question?A related question is a question created from another question. When the related question is created, it will be automatically linked to the original question.
This thread has been locked.
If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.
Hi Kingson,
Kmid is just the midband gain set by those resistors. Actually, my recommendation here is to use the LM5145 quickstart calculator to derive compensation values. Just ensure that the correct derated value with voltage for ceramic Cout is entered. The target crossover is usually 10-12% of switching frequency, and this affects Kmid as well.
Regards,
Tim
Hi Tim
Sorry, I make a wrong click vote down.
The answer you give me is not what I want.
Could you give me more details about "b" to "c" in the following picture ?
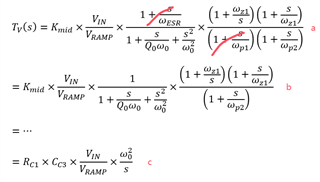
And more about the (15) and (16) ? thanks.

Hi Kingson,
See equation 18 and 19 here for more context on that derivation: https://www.edn.com/voltage-mode-control-and-compensation-intricacies-for-buck-regulators/. It's assumed the two compensator zeros are colocated with the LC double pole, which then results in a single-pole rolloff of the gain. Also, the high-frequency pole at Fsw/2 does not really impact the crossover at ~Fsw/10.
(15) to (16) is just straightforward simplification, where kff is the PWM ramp gain = Vin/Vramp (which is 15 for the LM5145).
Regards,
Tim
Hi Tim
I have studied your article in depth and known the formula 18;
But I still confused by formula 19, how to simplify from formula 18 to 19 by “fp1=fESR and fp2=fsw/2”?
I can understand a two-order system (formula 18) to one-order system (formula 19), but still can not understand the exist parameter “(wo)^2” or “(1/sqrt(LoCo))^2” (in formula 19 or LM5145 ds formula 14) ?
Bearing in mind that the pole located at fp1 cancels the zero located at fESR and the pole at fp2 is located well above crossover, the expression for Tv (s) specified by equation 13 and more explicitly by equation 18 can be manipulated to yield the simplified expression given by equation 19.
Hi Kingson,
Note that the two zeros cancel the LC double poles, thus leaving a single-order rolloff.
Regards,
Tim