Hello,
I want to detect a 200 nVrms signal at 30 kHz. For this purpose, I will build a circuit whose block diagram is shown below. First, I will take this signal and amplify it by 40 dB using a preamplifier (a low-pass amplifier with fc = 40 kHz). Then I will use a band-pass filter whose 0 dB passband is between 29 kHz and 31 kHz.
I wanted to perform a noise analysis of this system in order to determine whether the circuit can amplify a 200 nVrms signal in a meaningful way. I currently have two different approaches, and I would like to know which one is correct. For simplicity, in the noise calculations I will consider only the op-amp voltage noise. Again, for simplicity I will assume the voltage noise density of all op-amps is 1 nV/√Hz.
1 — First approach:
In this approach, I ignore the noise of the second stage BPF reflected back to the input, because its gain around the input is very small.
To find the input-referred noise of the first stage, I do the following:
For a signal with fc = 40 kHz, I approximate its noise bandwidth as 64 kHz.
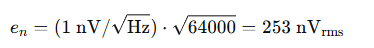
Using a Gaussian distribution assumption, I multiply this by 6.6 to estimate a peak value:
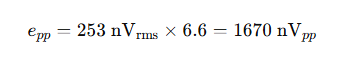
This means the op-amp’s noise is approximately 1670 nVpp, so the signal I want to measure will be buried inside this noise, and therefore I cannot measure this signal.
2 — Second approach:
As long as the system is operating linearly (i.e., the total voltage at the preamplifier output [signal + wideband noise] does not hit the op-amp supply rails and cause clipping/saturation), the signal is not destroyed by noise.
Signal and noise simply superimpose according to the superposition principle.
Since the op-amp’s output swing is in the volt range, this noise level will not saturate the preamplifier. Therefore, the signal will reach the second stage (the BPF) without distortion.
SNR Improvement:
The second-stage BPF will remove almost all of the wideband noise coming from the LNA, except for the small portion within the 29–31 kHz passband. Most of the noise power is outside this band and will be eliminated.
Result:
Because detection (or ADC sampling) will be performed after the BPF, the final system SNR must be calculated by integrating the noise power over the ENBW of the BPF, not the wideband noise of the first stage.


