Other Parts Discussed in Thread: ADS1220, ADS1256, ADS127L11
Hello
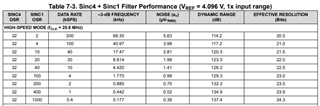
I have a general question ADS127L01 24 bit ADC. The maximum ENOB from the datasheet is only 21.83 bits at 2000 sps and max OSR of 2048.
Similarly I see other 24bit ADCs also but after looking through the datasheet their ENOB is only around 20-21 bits (ADS1220 advertised as 24 bit but 20.08 bit ENOB at 20sps).
There are some like the ADS1256 that truly achieve the 24bit ENOB with low data rates.
So wondering why ADS127L01 and ADS1220 are advertised as a 24 bit ADC. I must be missing something in their implementation or interpreting the datasheet incorrectly? I am hoping someone could help me with my understanding.
Thanks
Raghu