- Ask a related questionWhat is a related question?A related question is a question created from another question. When the related question is created, it will be automatically linked to the original question.
Hi experts,
I've watched videos in 'TI precision labs - ADCs' and benefited from it. But I'm still confused about some parameters of practical ADCs and their usage for my design.
As for ADS1281, I've got:
'f_mod' (sample rate as I understand): 1 MHz
data rate: 1000 SPS, for example.
FIR Bandwidth: 0.413 x 1000 = 413 Hz
(I'm personally interested in this kind of DC-optimized delta-sigma ADCs because of their high SNR, although it might be excess my need.)
Due to my unfamiliarity with delta-sigma ADC's principle, I'm confused about if these parameters suit my design, which is my main problem.
My input signal shows as follows:
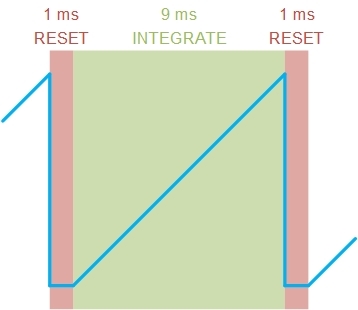
The sawtooth wave's period is 10 ms containing 9 ms "integrate" time and 1 ms for the "reset." I'm interested in the slope of the "integrate" phase.
These are my questions:
1. Is 1/2 of 'f_mod' the "input signal frequency range" without aliasing? Further, can the sampling accuracy (compared to the practical transient voltage) be guaranteed when input is less than 1/2 'f_mod'?
My input signal's upper limit frequency containing step components is about 30 kHz, which is much smaller than 0.5 MHz (1/2 f_mod), is which means each over-sampling point is accurate?
2. Because my signal has a step part, which parameters can I reference to ensure that the modulator can fastly follow the transient voltage reset? (Such as the 'slew rate' in OPAMP? But I can't find it in ADS1281's datasheet.)
Or it only depends on the input driver circuit's time constant? In this case, I think it's not a problem with proper design.
3. Will the low cut-off BW of the FIR filter lower my time-domain sampling accuracy?
I thought that the digital filter averages (decimates) 1024 over-sampling points (OSR) for one output data point. Hence in my plan A, I use a 1000 SPS data rate to sample my 100 Hz sawtooth wave, like the figure below, where I assume that the "selected data points" should be accurate.
(If I use a wide-band ADC and obtains much more data points as a plan B, eventually I still have to average them manually rather than utilize the integrated FIR filter)
But I'm worried about the feasibility of my design because I don't understand the 413 Hz FIR bandwidth's meaning. I tried to simulate it with an analog filter with the same BW, leading to an inaccurate output. So what does the FIR BW means? Will it influence my design accuracy?
Thank you!
Hello Robert,
1. Is 1/2 of 'f_mod' the "input signal frequency range" without aliasing? Further, can the sampling accuracy (compared to the practical transient voltage) be guaranteed when input is less than 1/2 'f_mod'?
I'm not actually sure what you mean by this question but let me see if I can still answer it. When I'm trying to understand bandwidth, I use this graphic (feel free to click on it for better quality).
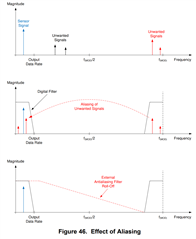
So f_MOD = 1.024MHz, f_MOD/2 = 512kHz and your current target data rate is 1kHz (so we can infer Oversampling Ratio is 1024). As you can see by the graph, I would define the "input signal frequency range" as something less than the data-rate. The area between the output data rate and f_MOD/2 is firmly in the stop band of the SINC filter. As you get closer to f_mod, that is the territory for aliasing to occur.
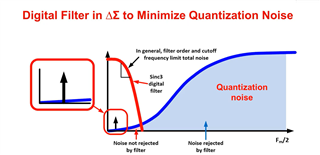
Correct me if I'm wrong but it looks like you missed the important of the concept of over-sampling. Oversampling is how we achieve SNR values on the delta-sigma ADCs. Below, you can see how we noise shape the the quantization noise closer to f_MOD/2 which is then rejected by the digital filter (which can be found in the Digital Filter TIPL video).
3. Will the low cut-off BW of the FIR filter lower my time-domain sampling accuracy?
Yes, if you go back to the "Effect of Aliasing" diagram above, you'll see the data-rate is actually higher above the -3dB bandwidth of the filter. This is why the FIR filter -3dB = 0.413*f_DATA (= 0.413*1000). Not to mention, the SINC filter's roll-off is technical more aggressive when looking at the -3dB so your effective bandwidth is even less.
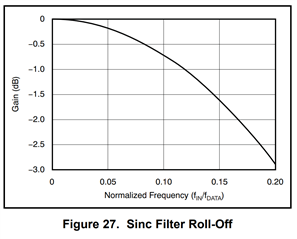
I actually just helped someone today where their data-rate was 4kSPS and their effective bandwidth was 1kHz. You should expect this when dealing with Delta-Sigma ADCs. You need a digital filter, whether its integrated into the ADC or not so you should expect getting an effective bandwidth less than your data-rate (because brick wall filters at the data-rate don't exist or have too high of latency to be useful).
2. Because my signal has a step part, which parameters can I reference to ensure that the modulator can fastly follow the transient voltage reset? (Such as the 'slew rate' in OPAMP? But I can't find it in ADS1281's datasheet.)
Its a good question, I'll personally need to double check. Lots of ADCs have the PGA integrated and you won't find a slew-rate parameter in those datasheets either. I think the assumption is that if you wanted to measure the signal, it should be in your bandwidth. If not, it will be attenuated (which means the PGA should have designed with a slew rate to support the largest full-scale range swing).
With that being said, the ADS1281 doesn't have a PGA so I can't make that assumption. The sampling frequency is much higher so, assuming the front end can provide charge to sample circuit, there is plenty of time for that capacitor to fill up and discharge. Again, I'll double check though. Edit: I've double checked at its fine. Just note if its in the stop band of the digital filter, it will be attenuated though that content was sampled by the modulator stage with no problem.
Comments about your Application:
I also want to let you know the ADS1282 device wasn't designed for DC measurements. Seismic customers usually add a low high pass filter to filter out DC and, the earth's surface doesn't move very fast so the high-bandwidth isn't useful in the application. We're missing typical features on this device that help you with DC measurement like a chopping feature or dedicated specification lines at DC.
Unfortunately, this precision vs. bandwidth is a trade-off as old as time. You mentioned maybe relaxing your SNR specifications in the other post. You might be better converting SNR into an ENOB table (which can then be translated into a voltage or current LSB), you'll know if your accuracy takes a hit.
As a general comment, the ADS1220 or ADS1262 are much more common in DC type applications. Not saying its a good fit, but it might be something to check out.
Best,
-Cole
edit: low to high pass, and notes about higher frequency sampling
