Because of the Thanksgiving holiday in the U.S., TI E2E™ design support forum responses may be delayed from November 25 through December 2. Thank you for your patience.

  • State Resolved
  • Locked Locked
  • Replies 6 replies
  • Subscribers 46 subscribers
  • Views 309 views
  • Users 0 members are here
Support feedback
Options
Options
Similar topics

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

DAC8162: Cause of Maximum Relative Accuracy

Shinichi Inoue
Guru 20486 points
Part Number: DAC8162
Other Parts Discussed in Thread: DAC8562

Dear Specialists,

My customer is considering DAC8162 and has a question.

I would be grateful if you could advise

---

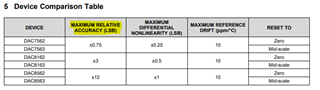
I have a question about the datasheet P.3 5 Device Comparison Table.

1)
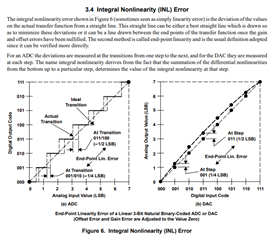
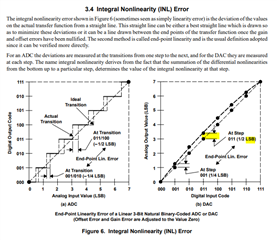
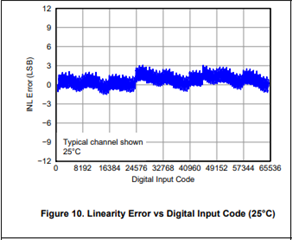
Regarding the integration error, the DACxx6x series consist of resistor string method.

In this case, what causes the errors to accumulate?

I think that the resistor string DAC basically does not generate an integral error(cumulative error)

2)
In case of DAC8562, the integration error is ±12.

I think that this number 12 corresponds to the lower bit 3 and 2. 

Why is the lower bit b1,0 ignored?

If the maximum integral (cumulative) error is the lower Bit b3,2, then b1,0 should also be affected, and the maximum would be ±15.

---

I appreciate your great help in advance.

Best regards,

Shinichi

  • +1
    TI__Mastermind 32588 points

    Hi Inoue-san,

    I think you are looking at the error that's listed as relative accuracy in the table. Is that right?

    The datasheet also calls this INL (integral nonlinearity) which is the deviation of each code from its ideal value on the DAC transfer function. This usually comes from resistors in the string not being the exact size. 

    The typ/max values given in the electrical characteristics table are the typ/max INL that you will see at any given code in the device. 

    I do not understand the second question. What do you mean by b3,2, and b1,0?

    Best,

    Katlynne Jones 

  • 0 in reply to Katlynne Jones
    Guru 20486 points

    Hi Katlynne,

    Thank you for your reply.

    1) Yes, the customer is looking at the table you mentioned.

    2) b3,2,1,0 is a bit number 

    b0 is LSB, b1 is LSB+1bit, b2 is LSB+2bit, b3 is LSB+3bit.

    Each bit weight, b0=1, b1=2, b2=4, b3=8.

    +/-12LSB is b2=1 and b3=1, the customer think why b0 and b1 are 1.

    They think INL error becomes 15LSBs in this case. 

    So the customer'd like to know the reason.

    I appreciate your great help and cooperation.

    Best regards,

    Shinichi 

  • +1 in reply to Shinichi Inoue
    TI__Mastermind 32588 points

    Hi Inoue-san,

    I understand. That is not how we measure/calculate INL. The INL does not directly correspond to the weighted bits/switches on the resistor ladder and we also don't determine the max error to be the worst case of a certain number of bits being equal to one. I think maybe that is what the customer is assuming. From the figure I shared in my last response, the INL is normalized to the end points so the maximum INL error occurs at mid code. This is because the accumulated errors due to the variance in resistor sizes is the worst at this point (mid code) if we consider the error at the endpoints to be zero. In the example from the figure, the maximum error would correspond to the difference between the actual measured output and the ideal output that would be calculated by the DAC transfer function at mid code. If we know the resolution and reference of the DAC then we can translate the 12LSB error to a error in volts. 

    The typical INL curve for this device is shown in the typical characteristics section of the datasheet. It looks like this device has some INL correction (or trimming) being applied in different segments. So the endpoints of each section are corrected to close to zero, and the mid points of each section should see the accumulated error. The 12LSB max spec just means that any code is guaranteed to be less than 12LSBs off from the ideal value. 

    Best,

    Katlynne Jones

  • 0
    Guru 20486 points

    Hi Katlynne,

    Thank you for your reply.

    I understand.

    Integral Nonlinearity does not directly correspond to the weighted bits/switches on the resistor ladder

    and  INL is the difference between the actual measured output.

    I'll share your answer with the customer.

    When the customer has an additional question. I consult you again.

    I appreciate your great help and cooperation.

    Best regards,

    Shinichi

  • +1 in reply to Shinichi Inoue
    TI__Mastermind 32588 points

    Hi Inoue-san,

    I will close this thread for now. Please respond here or start a new thread later if they come back with more questions.

    Best,

    Katlynne Jones 

  • 0 in reply to Katlynne Jones
    Guru 20486 points

    Hi Katlynne,

    I agree.

    Let’s close this thread.

    When the customer has an additional question, I consult another thread.

    Thank you for your great support.

    Best regards,

    Shinichi