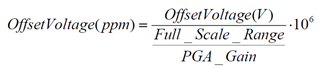Hi,
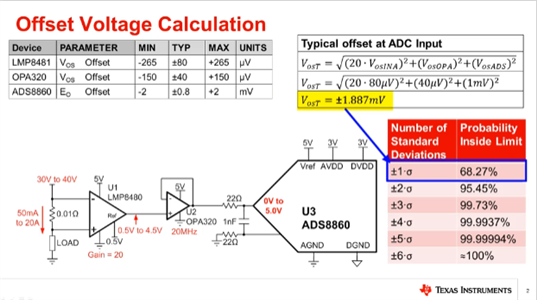
I am doing a tolerance Calculation of a circuit using this ADC. It seems, that the offset error is dominating my tolerance.

I interpret the value of +/-3mV (both ranges) as maximum over operating temperature (-40°C to 125°C)
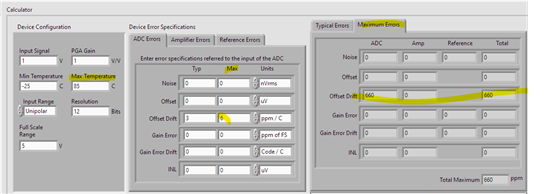
As my design would not see that high temperatur range, I think, I can use a smaller min/max value when I it calculate with the offset error temperature drift of +/- 3ppm/°C.
But I don't know how to calculate it.
Or more precice, when 3ppm is the same as 0.0003%, what is the value of 100%.


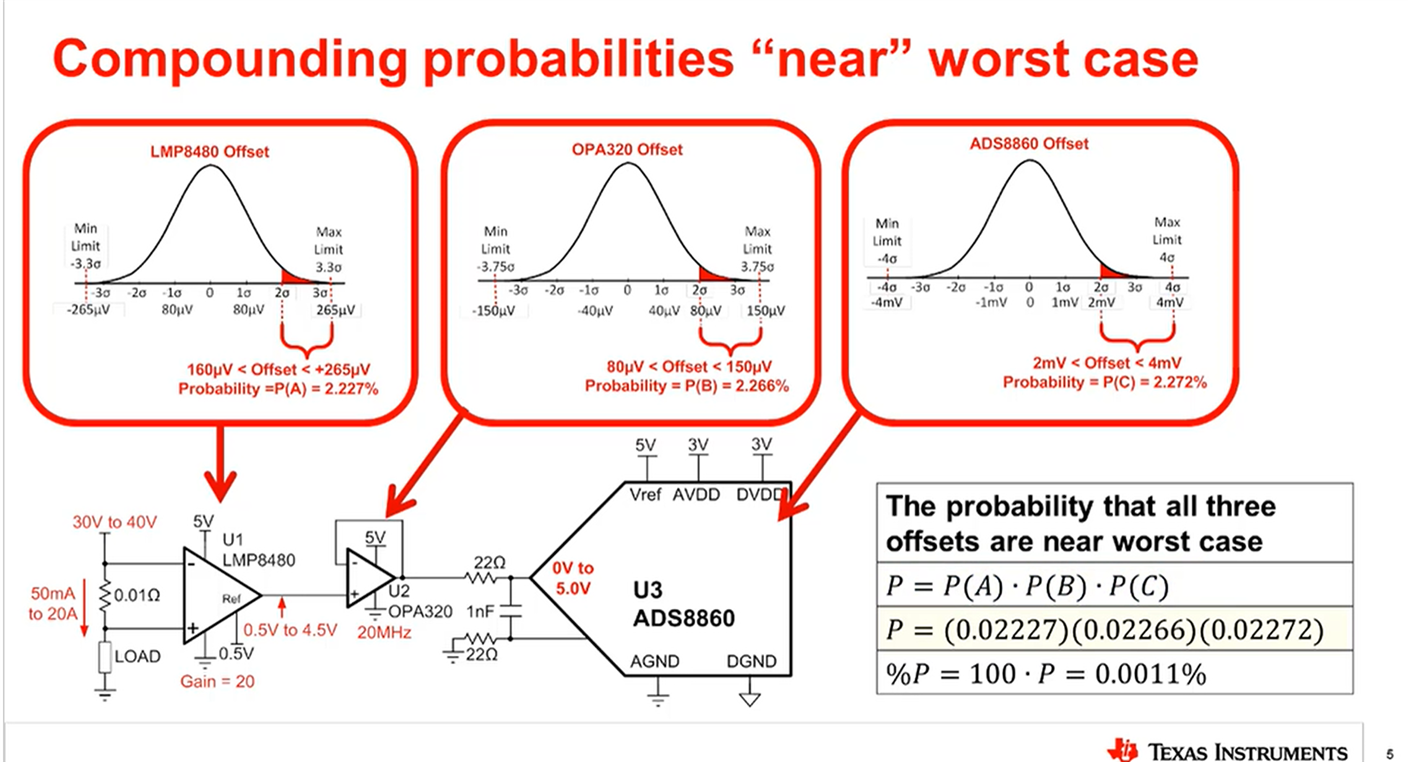
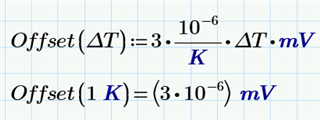 the same value as your explanation.
the same value as your explanation.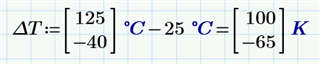
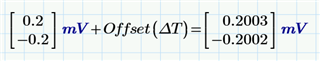 I didn't expect to hit +/-3mV, but I didn´t expect to be factor ~15 away.
I didn't expect to hit +/-3mV, but I didn´t expect to be factor ~15 away.