Tool/software:
Hi
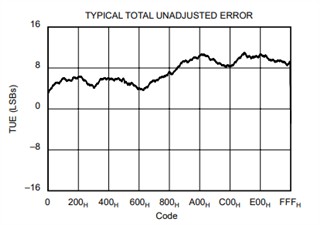
When calculating the Total Unadjusted Error (TUE) for a DAC is the same method as used for an ADC i.e. the same as described in 'ADC Performance Parameters - Convert the Units Correctly!' (Application Report SLAA587 - May 2013),
Br
Edba