12bits or 16bits? ADC's SNR and NSD

min hu,

We are looking into this.

Regards,

Jim

Hello.
the ideal ADC is limited by quantization noise as you stated. The real adc has additional noise contributors such as thermal noise and clock noise for example.
Thermal noise is highly dependent on the signal amplitude. Precision adcs often can accept very large input signals (e.g. 8Vpp) which enables to achieve very low noise. Highspeed ADCs primarily focus on faster sampling rates and higher bandwidth and trade off SNR for power consumption. That's why the SNR of highspeed ADCs often is quite far from the ideal SNR. In addition the core ADC resolution has a direct impact on the higher order harmonic spur performance which is important for wide band applications.

In the examples you listed.
ADS54J60: 16bit with thermal noise ~ 71.5dB and non HD2,3 performance ~ 90dB
ADS5400: 12bit with thermal noise ~ 59.5dB and non HD2,3 performance of ~ 80dB

At higher input frequencies (e.g. 470/600MHz listed) the noise floor becomes almost completely dominated by the clock noise. If you were to go to ~ 2GHz input you wouldn't be able to tell a difference at all anymore between 12 or 16bit as noise floor is entirely dominated by clock noise.

In regards to your questions:
1. ADS54J60 is 16 bits and ADS5400 is 12 bits,but the SNR difference is 8dBc, the 16 bits ADC does not seem to have a significant perforance advantage since it is much more expensive??? why N matters???
SNR (thermal noise) difference is ~ 12dB which is a huge delta. Also note difference in non HD2,3 performance.

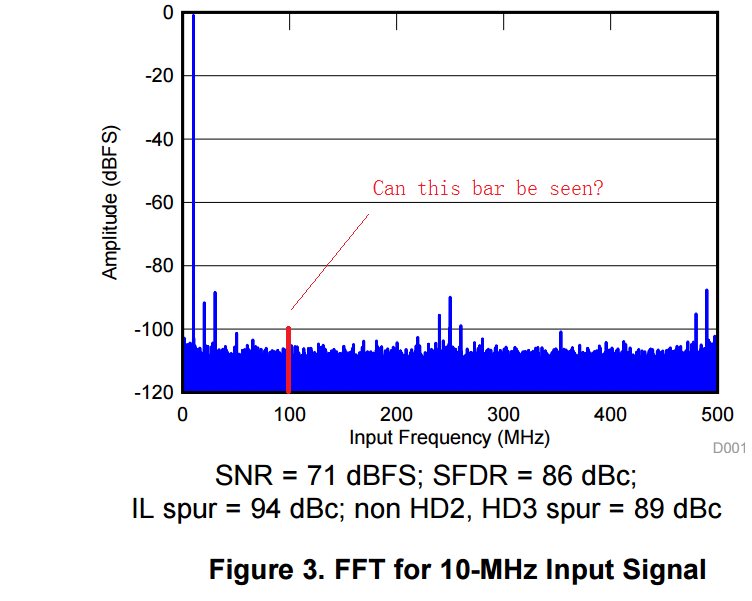
2.if input signal is 6.02*16 = 96.32 dB lower than FS but higher than NSD,e.g. a 100MHz input is -100dBFS(or even lower,FFT Gain is high enough),Can ADS54J60 'receive' this input???
ADS54j60 has a noise floor of ~ -156dBFS/Hz. You should be able to detect signals at -100dBFS.
If you wanted to see it in the FFT you can:
- lower noise floor in FFT by increasing FFT size and add averaging
- high order ADC harmonic spur performance becomes critical for low amplitude spurs

Hi 

----------------------------------------------------------------------------------------------------------

ADS54j60 has a noise floor of ~ -156dBFS/Hz. You should be able to detect signals at -100dBFS.
If you wanted to see it in the FFT you can:
- lower noise floor in FFT by increasing FFT size and add averaging
- high order ADC harmonic spur performance becomes critical for low amplitude spurs

--------------------------------------------------------------------------------------------------------

I still have questions about this:

the minimum input power for 'quantization units' should be   -96.32 dBFS(6.02*16) for 16 bits ADCs(e.g. ADS54J60), a ideal adc should gets all '0's for input lower than -96.32dBFS,with -100dBFS input or below(Assuming:a ADC chip is perfectly designed and additional noise contributors such as thermal noise and clock noise are incredibly low),output digital sample code is all '0's !??

there should be no spectrum line because all '0's carry no information !??

Hi again.
For a single sample you are correct. The min you can detect is given by the quantization noise.
FFT processing however uses multiple samples to give the result. Similar you could use averaging to improve the result by lowering the noise. Imaging taking 2 samples, one with result 0000 and second with 0001. You average to samples and result is 0.5 which is below min quantization noise of the ADC itself. The sigma delta ADC uses that same principle where the quantizer is using a single bit but the true result is after digital filtering.
With ADS54j60 if you took 1 single sample the min signal you could detect is around 71dBFS, the thermal noise of the ADC. Once you add averaging or post processing you can reduce noise further

Hi

thanks for your reply.

you are right !

 I got stuck in the quantization noise floor: '6.02N + 1.76', the lowest input power level can bu much lower.

Hoo