Other Parts Discussed in Thread: THS4531, ADS8321
Hello,
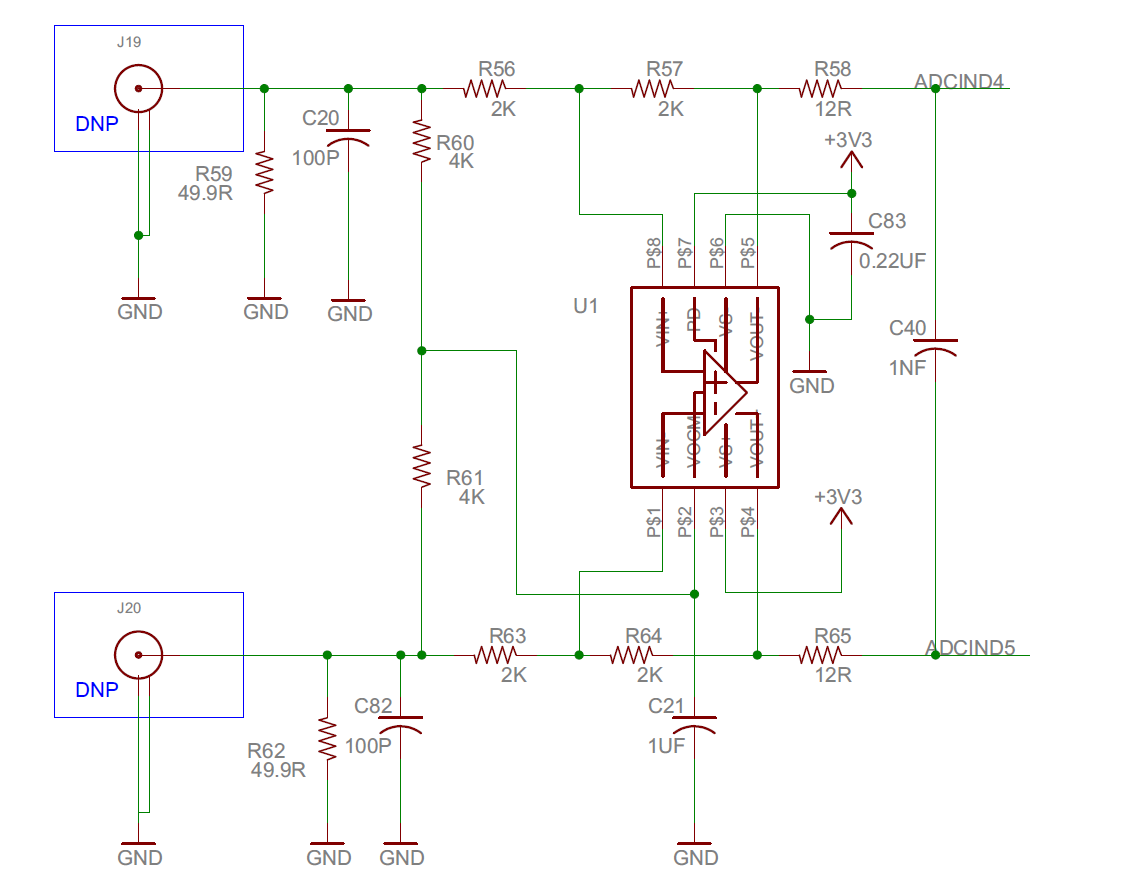
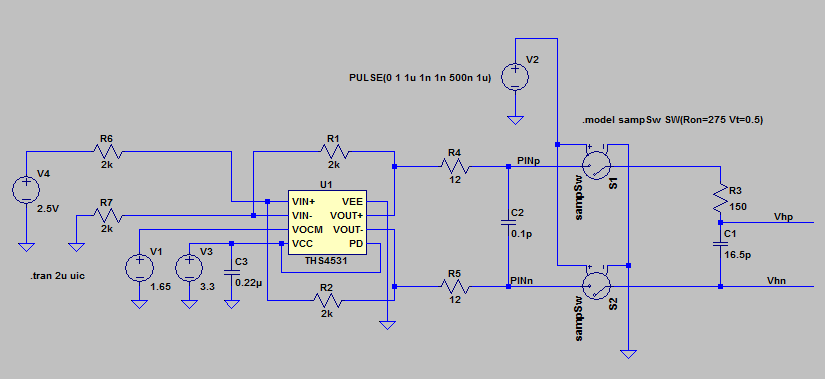
I have a couple of questions concerning the op amp circuit that is included on one of the ADC differential channels on the 28379D launch pad. I have included a snap shot of the relevant part of the circuit below. This was taken from the user guide.
My issues are:
1. The Vocm pin on the op-amp (pin 2) sets the output common mode voltage. Usually I have seen this set to half the supply, or derived from the reference voltage used by the ADC. Here it is set to the input common mode voltage. I wonder if this was intended and if so what advantage it gives. There is a precision reference source on the board, is there any reason why Vocm was not derived from that?
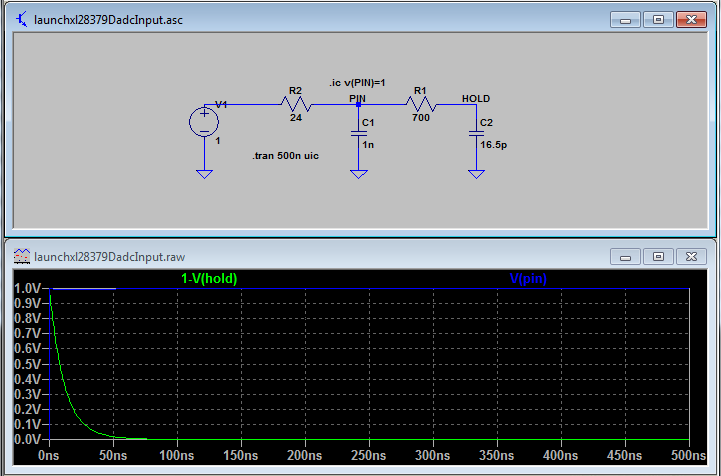
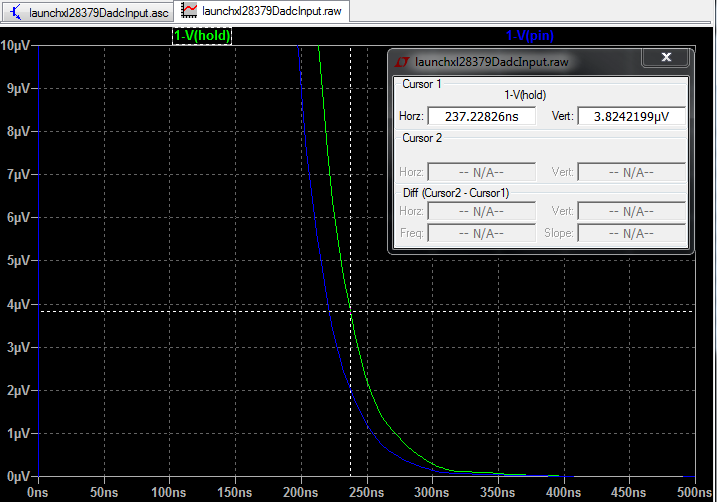
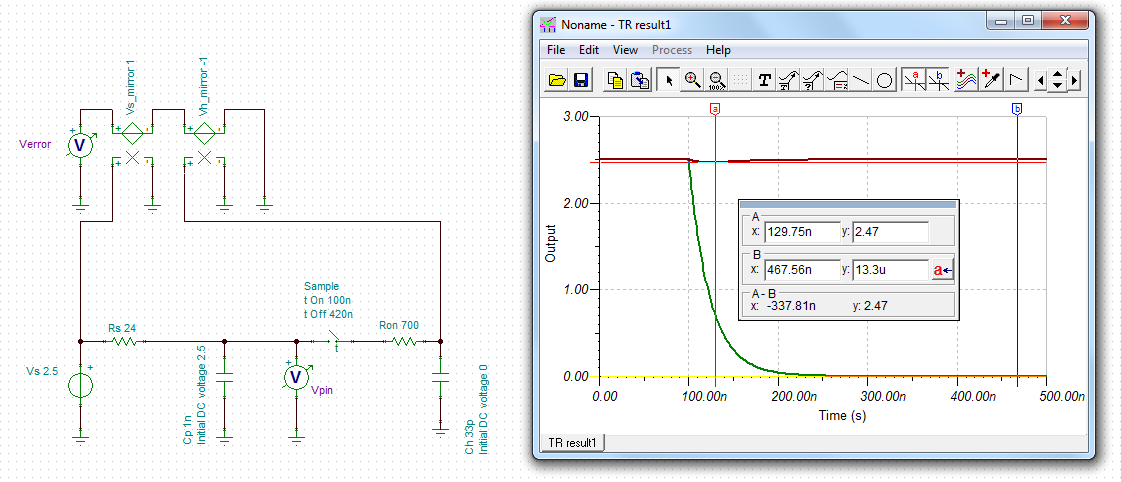
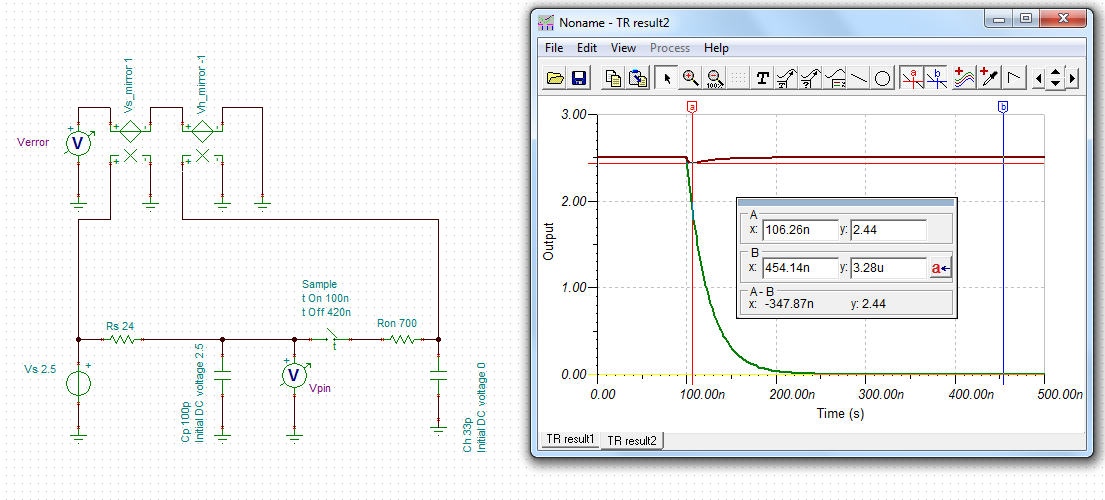
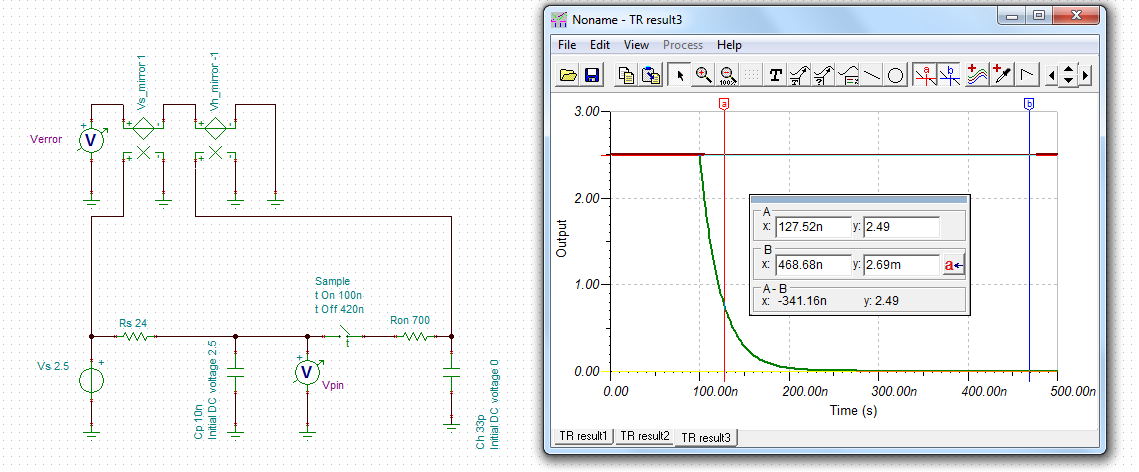
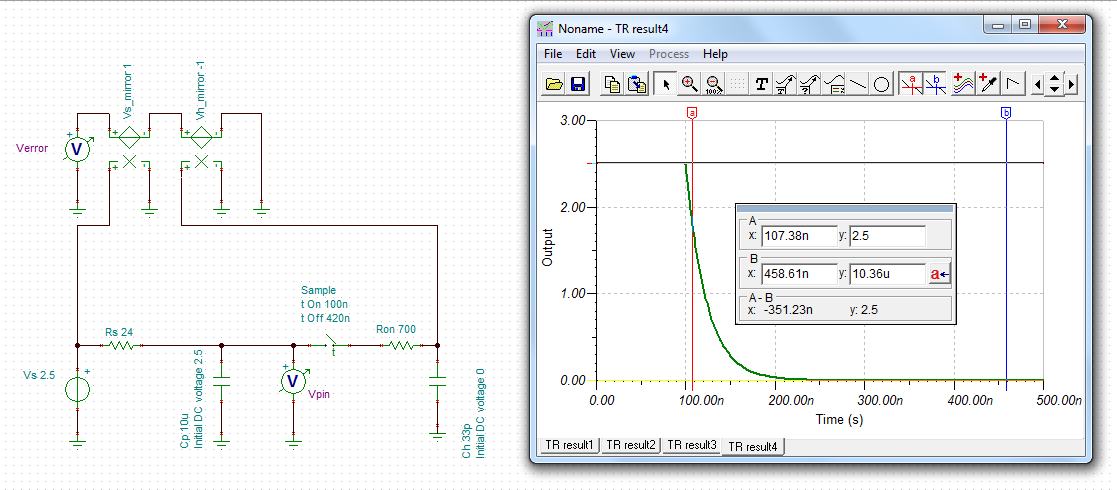
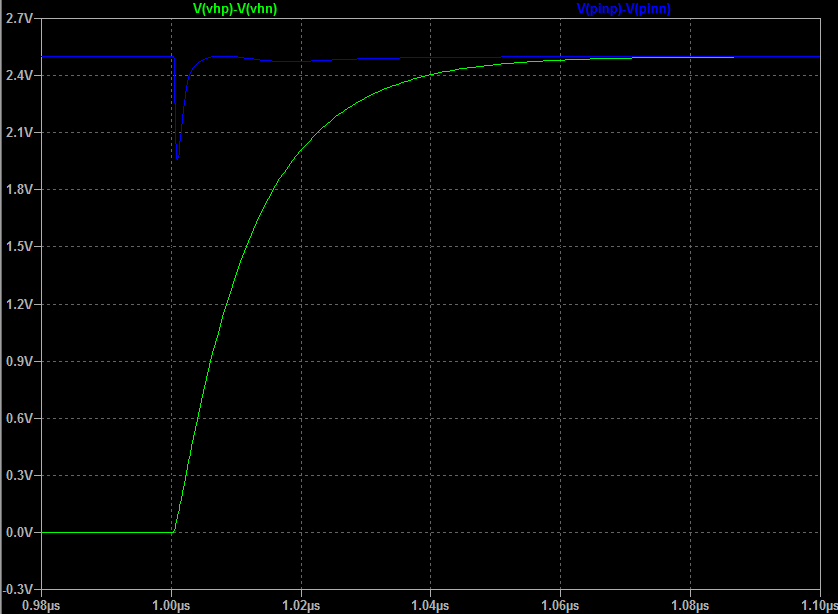
2.Each input has 50Ω and 100pF in parallel. This looks a bit odd to me as the resistor it gives a DC termination of 50Ω and the capacitor could cause problems to whatever is driving the input. The application notes in the data sheet for the op amp (THS4531) shows an input circuit that has the resistor and capacitor in series and this makes more sense. Is the configuration on the launch pad a mistake? If not what is the reasoning behind it?
Thanks for your help.
John Wilkes.