• State Resolved
  • Locked Locked
  • Replies 5 replies
  • Subscribers 83 subscribers
  • Views 1701 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

TMS320F28377D: Incorrect FFT output using example project?

dduncan
Intellectual 315 points
Part Number: TMS320F28377D
Other Parts Discussed in Thread: CONTROLSUITE

I'm not understanding why I'm getting unexpected results when using the TI FFT library.  Using the 2837x_vcu2_rfft_512 example project (from v2_10_00_00 in ControlSUITE 3.4.6).  Here are the steps to reproduce:

1) Load CCS 7.1.0.00016.

2) Load the debugger without making any modification to the example project.

3) Set a breakpoint on the I the init() call and run to that line.

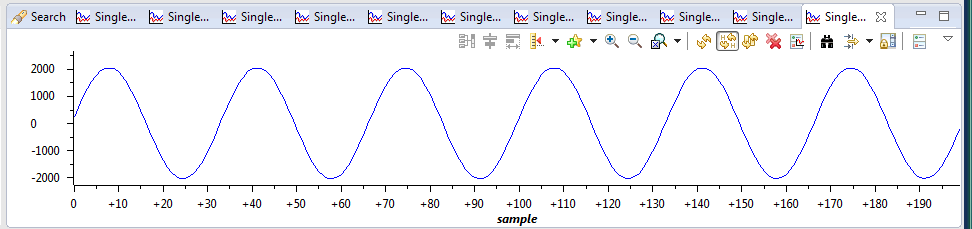
4) Use the "Load Memory" feature of the memory browser to load the attached input file to buffer1Q15, then graphed here:

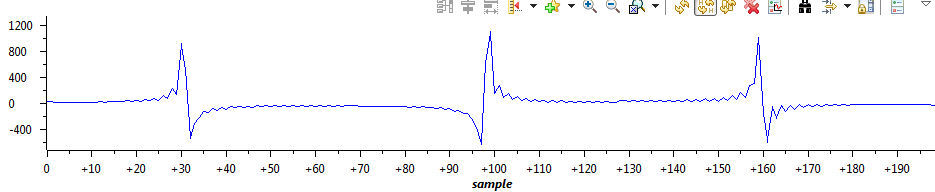
5) Run a couple lines further, to after the unpack() call.  The output in buffer2Q15 is here:

The input is generated using a hardware signal generator, so it's not perfect, but one wouldn't expect to see any substantial spikes outside of the first one.  (Indeed, a Matlab FFT on the same input data is similar to as described.)  I haven't experimented extensively, but in my original application when the sampling rate was 100 KHz with a 3 KHz sine wave, I'd see what looked like the odd harmonics; with 100 KHz and 4 KHz, it looked like the additional spikes were the even harmonics.

Am I overlooking something, or is this a bug related to the FFT library?  Thanks.

-David

example_code_input.dat

  • 0
    TI__Mastermind 20850 points

    David,

    I ran the example with your data and got just the fundamental.

    Step 1: I loaded the data in the manner you described

    Step 2: I setup a dual graph to show 512 points of unsigned int, buffer1Q15 in the top graph, buffer2Q15 in the bottom graph

    Step 3: After run()

    Step 4: after unpack()

    Looking at buffer1Q15 i see the complex spectrum, if we were to take the magnitude you would see the fundamental in the 15th bin, which works out to 15*(100e3/512) = 2929.6875 ~ 3KHz, plus some leakage around the fundamental.

  • 0 in reply to Vishal_Coelho
    Intellectual 315 points
    Great, thanks for the help. So it seems the key is that I was looking in the wrong buffer, which of course seems simple now . :) For what it's worth, I'd suggest that it's worthwhile to make the document clearer. CFFT_unpack() is described in the user guide and code with "This is an in-place algorithm; the routine writes the output to the input buffer itself"; this is, at the very best, likely misleading.

    And just for clarity, when you say the 15th bin, you mean ~31st bin, correct? As I understand it, when the output is not mirrored, it'd be 31*((100e3 / 2)/512) = ~3KHz.

    Also, could you share how you get the graph to show all 512 points?
  • 0 in reply to dduncan
    Intellectual 315 points

    dduncan said:
    For what it's worth, I'd suggest that it's worthwhile to make the document clearer. CFFT_unpack() is described in the user guide and code with "This is an in-place algorithm; the routine writes the output to the input buffer itself"; this is, at the very best, likely misleading.

    Actually, while potentially the statement I quoted could be a little unclear, I maybe better understand now--the run() function is presumably considered "in-place" as well (though it makes use of the other buffer).  I guess while the documentation could be more clear, this makes sense, and the fault is as much with me for not leaving better comments for myself with my original implementation a good while back.

  • 0 in reply to dduncan
    TI__Mastermind 20850 points

    dduncan said:
    the run() function is presumably considered "in-place" as well (though it makes use of the other buffer).  

    The run() is off-place. It needs two buffers, switching the input and output buffers every 2 stages of the FFT, so you end up losing the original input in buffer1Q15. The FFT structure maintains two points pIn and pOut to keep track of the input and outputs at each stage; saves you the trouble of keeping track of the final output, pOut should always point to where the output is (could be buffer1Q15 or buffer2Q15 depending on the size of the FFT).

    Now unpack() is in-place. It takes as its input the output (whatever pOut points to after run()) from the run() and does its thing on that buffer.

  • 0 in reply to Vishal_Coelho
    Intellectual 315 points

    Thanks, that seems like a very good explanation.  I didn't realize the number of stages mattered; I had somehow got to thinking that the ping-ponging was just between consecutive calls to the library.