Hello,
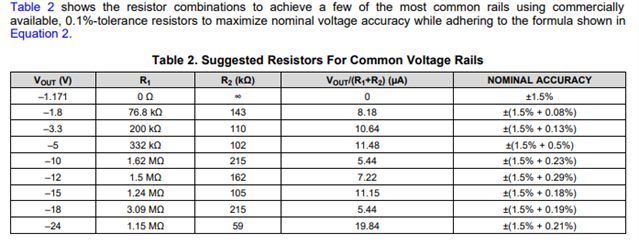
I have several questions for Table 2, Suggrestiged Resistors For Common Voltage Rails, in the datasheet(SBVS169D) of TPS7A33.
When R1 = 0 ohm and R2 = Open case, the table says that VOUT = -1.171V. But NOM VREF value should be -1.175.
Why is VOUT -1.171V instead of -1.175V?
For other VOUT casees, I can't understand how to calculate NOMINAL ACCURACY value.
For example, VOUT = - 3.3V case.
VOUT is calculated: 1.171 * (200K + 110K)/110K = 3.300090909V. Then 9.09e-5/3.3 * 100 = 0.00275%
When using 1.175V for VREF, 1.175 * (200K + 110K)/110K = 3.311363636. Then 0.011365/3.3 * 100 = 0.34%
Both are not 0.13%.
Where this NOMINARL ACCURACY come from?
Regards,
Oba