• State Resolved
  • Locked Locked
  • Replies 1 reply
  • Subscribers 64 subscribers
  • Views 175 views
  • Users 0 members are here
Support feedback
Options
Options
Similar topics

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

TPS7A33: Table 2 in the datasheet

Oba
Genius 16565 points
Part Number: TPS7A33

Hello,

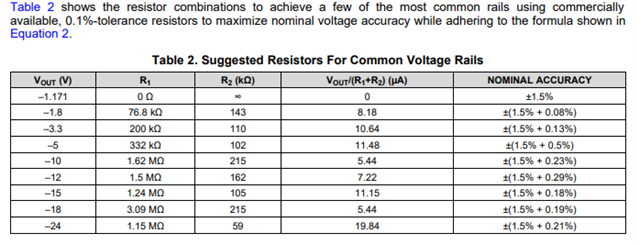
I have several questions for Table 2, Suggrestiged Resistors For Common Voltage Rails,  in the datasheet(SBVS169D) of TPS7A33.

When R1 = 0 ohm and R2 = Open case, the table says that VOUT = -1.171V.  But NOM VREF value should be -1.175.
Why is VOUT -1.171V instead of -1.175V?

For other  VOUT casees, I can't understand how to calculate NOMINAL ACCURACY value.

For example, VOUT = - 3.3V case.

VOUT is calculated: 1.171 * (200K + 110K)/110K = 3.300090909V. Then 9.09e-5/3.3 * 100 = 0.00275%
When using 1.175V for VREF, 1.175 * (200K + 110K)/110K = 3.311363636. Then 0.011365/3.3 * 100 = 0.34%

Both are not 0.13%.

Where this NOMINARL ACCURACY come from?

Regards,
Oba

  • +1
    TI__Genius 12511 points

    Hi Oba,

    I am unsure as to why the Vout short to FB is at 1.171, this seems to be a typographical error in the parts datasheet, you are correct in that by shorting VOUT to VFB and opening R2, VOUT will be regulated to VREF = -1.175.

    As for the nominal accuracy calculations:

    The nominal accuracy is a summation of the parts inherent accuracy for the bandgap and internal function of +-1.5% then the additional percentage, 0.13% in the VOUT = -3.3V case, is computed by utilizing 0.1% resistors as stated above:

    So for the -3.3V the math is computed as follows if worst case is assumed where R2 is a full 0.1% above it's specified value, and R1 is a full 0.1% below it's specified value:

    1.175*(200000+110000)/110000 = 3.31136363636

    1.175*(200000*0.999+110000*1.001)/(110000*1.001) = 3.30709517755

    3.30709517755/3.31136363636 = 0.998710966453

    1 - 0.998710966453 = 0.001289033547 = 0.1289% which is rounded to 2 significant digits in the table up to 0.13%

    This also works the other way with the R2 being 0.1% below it's specified value, and R1 is a full 0.1% above it's specified value:

    1.175*(200000*1.001+110000*0.999)/(110000*0.999) = 3.31564064064

    3.3156406406/3.31136363636 = 1.00129161419

    1 - 1.00129161419 = 0.00129161419 = 0.1291% which is rounded to 2 significant digits in the table up to 0.13%

    Regards,

    John