Tool/software:
Hi, TI
How to select input capacitors for a buck converter slyt670 How to select input capacitors for a buck converter
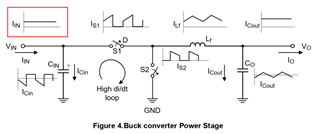
From slyt670, we know the calculation of Cin(min) is the Equation (1) with D = Vout / Vin.
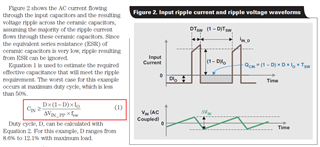
But, why there is no (1-D) in equation 11 Cin(min) of TPS40345?