LM1117: Thermal calculate of LM1117I

Hi Leo,

1. At the operating point you mentioned, the power dissipation is 1.2W. Whether or not thermal shutdown is reached depends on the ambient temperature and the case temperature prior to the operating point (this can be different from ambient if a heat gun was waved at the device). At 1.2W dissipation, the rise in junction temperature above ambient temperature is 74°C for the DCY package. The device can go into thermal shutdown if ambient temperature is greater than 76°C.  Please look at section 9.5.1.1 from the datasheet for more details on this topic.

If Vout decreases to 0 quickly, I assume you mean a short to GND at the output. The device follows a brickwall current limiting scheme as shown in fig 7-2 of the datasheet. Iout will spike to a value equal to Vout/R_ds (pass element) where R_ds is the drain to source resistance of the pass FET right before the short event. The current limiting is not instantaneous, and a delay of a few microseconds will elapse before the short circuit current limit kicks in. At this value of Iout = 1.2A, power dissipation is 8.4W. The device will go into thermal shutdown.

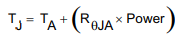2. The correct equation is where Power is the power dissipation. However, RθJA is a variable function of not just the package, but of many other system level characteristics such as the design and layout of the printed circuit board (PCB) on which the part is mounted. Also note that .

So, if you have the case temperature, you can work off the above two equations.

Best regards

Ishaan