Other Parts Discussed in Thread: TPS61094
Tool/software:
Hi experts,
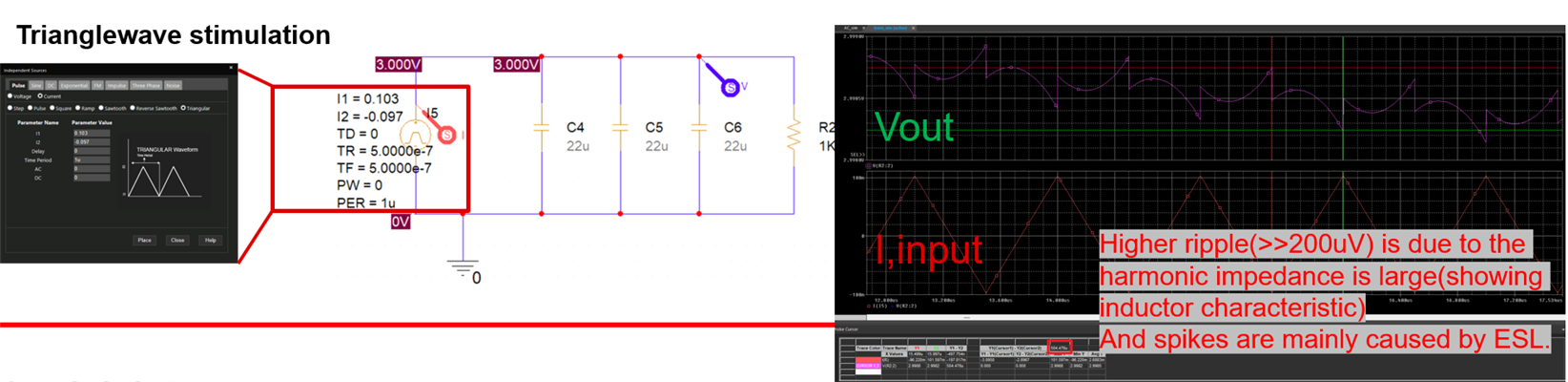
The theoretical value of Vout,ripple doesn’t match the measured result when I use TPS61094 EVM to run the test of Figure8-2 from datasheet(TPS61094 60-nA Quiescent Current Boost Converter with Supercap Management datasheet (Rev. C)).
The test condition is set Vout and Vin unchanged, increasing Iout by adjusting E-load, and get Vout,ripple from different load cases.
Measurement setup looks like this:

The vout,ripple formula derivation ref source is Basic Calculation of a Boost Converter's Power Stage (Rev. D)

Below is the measured result:
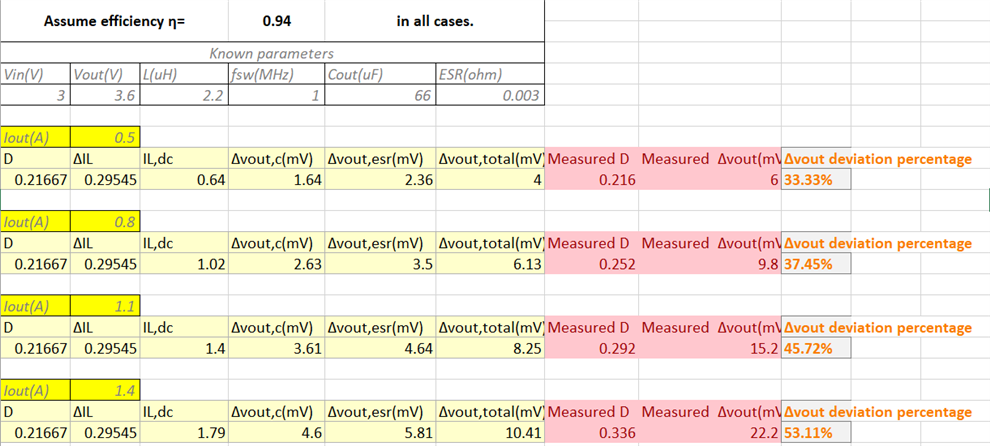
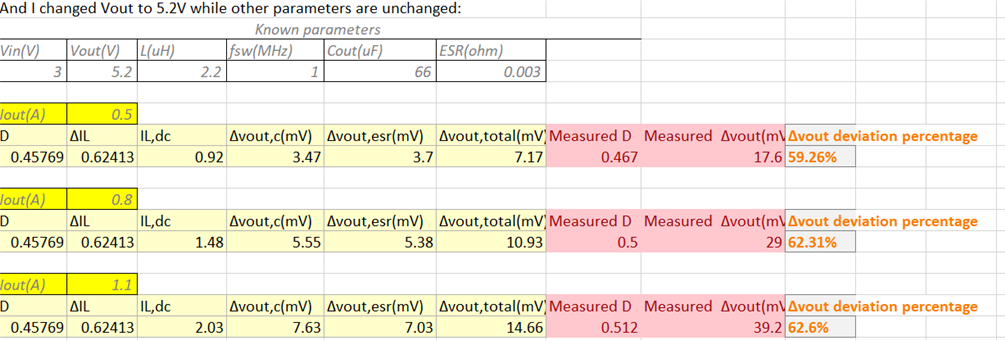
How to explain the deviation between measured result and theoretical Vout,ripple value, especially when Iout increasing?
Another thing is, the Cout that used in EVM is operating at the self-oscillating point where fsw is about 1MHz in TPS61094, so Cout should now be treated as a pure R with magnitude of ESR, there will be no Δvout on C, just Δvout on ESR, then the deviation escalates.

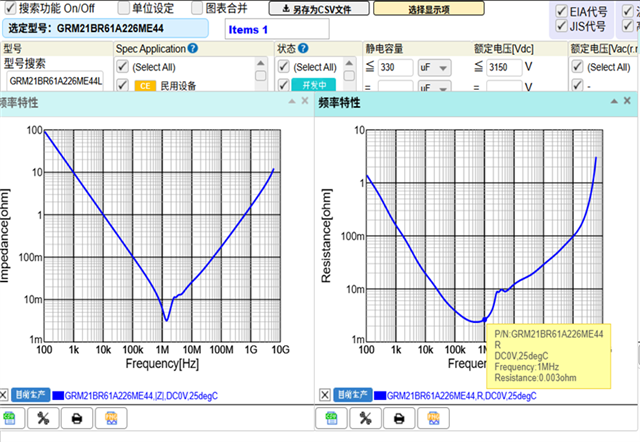
Looking forward to your reply.
Best Regards,
Ethan