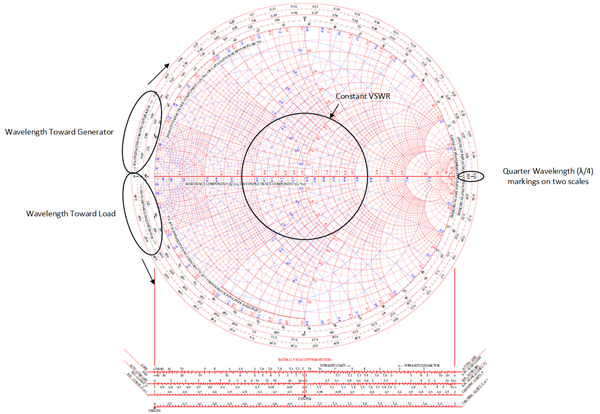
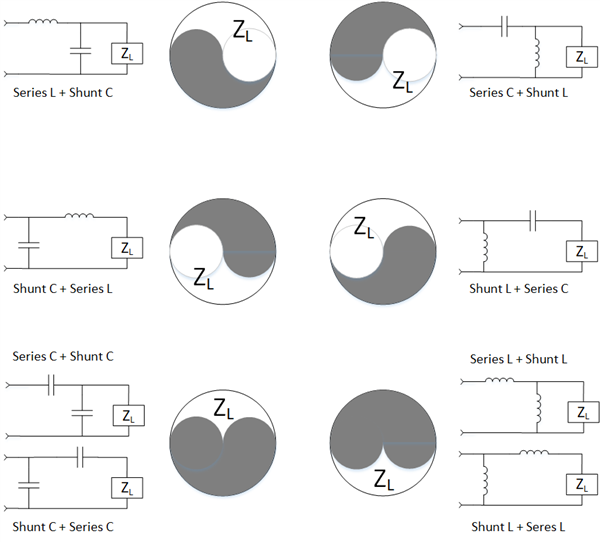
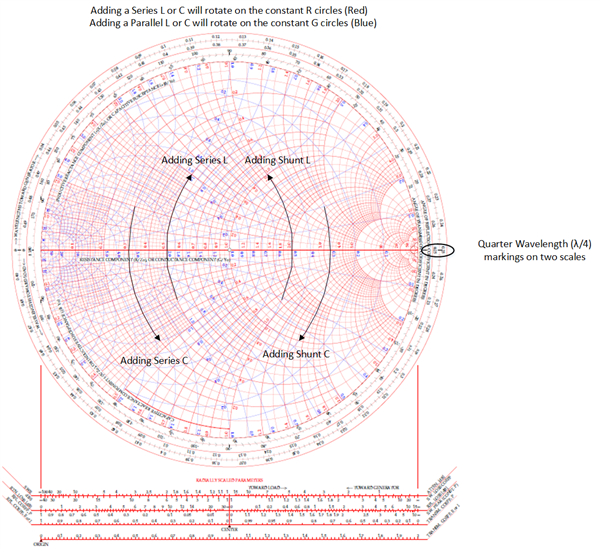
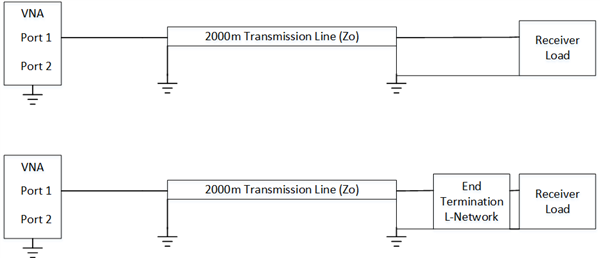
My apologies if this isn't the most appropriate forum to ask this question, but I have found the response from users on this form to be extremely helpful in the past with my electrical questions.
I am new to impedance balancing so bear with me. I have a transmitter and receiver with 2000 meters of electrical cable connecting the two. The signal I am transmitting is a 3.3 volt digital signal. I am trying to impedance balance this network and a bit confused where to hook up my VNA. I drew a diagram below, is this correct? If I understand it, my VNA connects to the transmitter circuit while it is connected to the 2000 m transmission cable, which is then connected to the receiving circuit. Using my VNA and a Smith Chart, I will impedance balance the TX circuit with some "L" network including a certain value inductor and capacitor. After that is balanced on the VNA, I connect my VNA at the receiving end and do the same type of impedance balance.
Does this make sense or am I going about this wrong? Thanks for any input anyone has.