• State TI Thinks Resolved
  • Locked Locked
  • Replies 5 replies
  • Answers 1 answer
  • Subscribers 63 subscribers
  • Views 637 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

BQ4050: CEDV Worst Error for Aged Batteries

nopancakes
Prodigy 170 points
Part Number: BQ4050
Other Parts Discussed in Thread: BQ40Z50

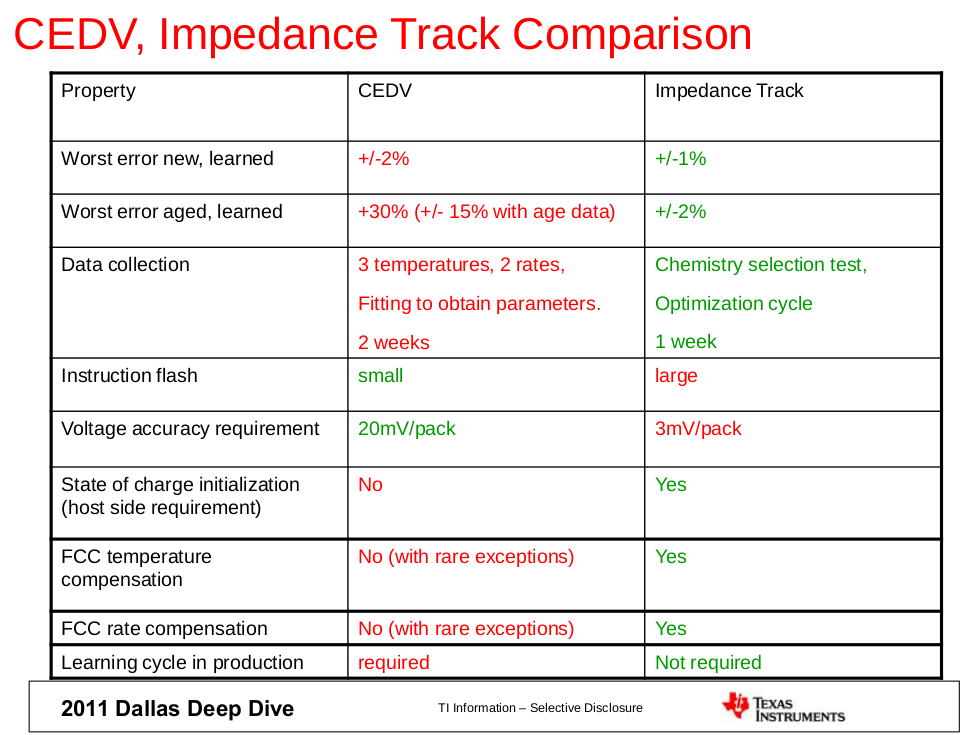
Slide 36 from 2011 Dallas Deep Dive tutorial on Gauging Algorithm Comparisons provides a side-by-side comparison table of CEDV vs Impedance Track algorithms. The 'Worst error aged, learned' property of CEDV is given as +30% (+/- 15% with age data), which is pretty high and is substantially higher than that of Impedance Track. I would like to ask a few related questions.

1. What exactly does 'Worst error aged, learned: +30% (+/- 15% with age data)' mean? Does 'learned' imply a learning cycle has been performed? What's the age data? Is it number of cycles?

2. What are the conditions that result in the worst case error of 30% for aged batteries? 
I know that CEDV updates FCC when the battery discharges to about 7%, so does one arrive to the worst case estimate by never allowing qualified discharges or is there something else involved?

3. Is this error accounted for in MaxError() that bq4050 reports? I.e. if my battery aged and I have the worst case +30% error, is the output of MaxError() going to be 30%?

Our application demands very few relaxation periods and high (5-10C) discharge currents, it seems a CEDV gauge such as bq4050 suits it better than bq40z50.

Thank you in advance,

Vasily

  • 0
    TI__Mastermind 24870 points

    Hello Vasily,

    These errors are most likely derived from one set of lab data.

    In actual operation for gauging, the error is really based on inaccuracy of prediction. This really depends on the use case.

    MaxError is defined in the TRM on a per cycle basis. It could go up to 100% if the gauge does not under go any EDV correction.

  • 0 in reply to Kang Kang
    Prodigy 170 points

    Hi Kang Kang,

    Thank you for a clarification but I don't know how to interpret this sentence: "In actual operation for gauging, the error is really based on inaccuracy of prediction." So how do you quantify this inaccuracy of prediction? Please explain what you meant.

    If SoC prediction accuracy of BQ4050 degrades to a +-15% error over time, I'd really like to know that in advance. I want to understand

    • what factors affect this error as the battery ages
    • how to quantify this error
    • over how many cycles this error starts to emerge and
    • whether I can take any measures to reduce this error (i.e. perform periodic deep discharge-charge cycles, etc)

    Thank you in advance!

    Vasily

  • 0 in reply to nopancakes
    TI__Mastermind 24870 points

    Hello Vasily,

    Yes, these are good questions.

    The CEDV algorithm tries to predict when the battery will hit EDV2 with "compensation" for age, temperature.

    To quantify this error relies on testing and data in system. My suggestion would be to test it over some sample size of battery packs and determine what the worst case error is in your system.

    In terms of reducing the error, you could try and make sure the gauge and battery go through full charge cycles, however, there's no exact way as it is system dependent on how often you get the gauge to recalibrate to EDV2 and EDV1 and EDV0 points.

    Thanks!

  • 0 in reply to Kang Kang
    Prodigy 170 points

    Hi Kang Kang,

    Thank you for following up promptly.

    I see, fair enough. Then in order to asses the errors based on my test data I need some sort of a ground truth about the SoC of an ageing battery. Can you please recommend a good approach for obtaining this ground truth? I imagine the best estimate about the 'real' battery capacity comes from using high-precision current integrator (e.g. a programmable load with a good coulomb counter) but I may be missing something. One needs to still account for charging losses / compensate RM for temperature/current.

    • What other equipment / approaches you can recommend?
    • What do you use at TI to get reference state of charge of a battery?

    Thank you in advance,

    Vasily

  • 0 in reply to nopancakes
    TI__Mastermind 24870 points

    Hello Vasily,

    Some approaches could be to use an automated battery cycler.

    For TI, we get reference SOC by doing coulomb counting from when the charge termination conditions are met.