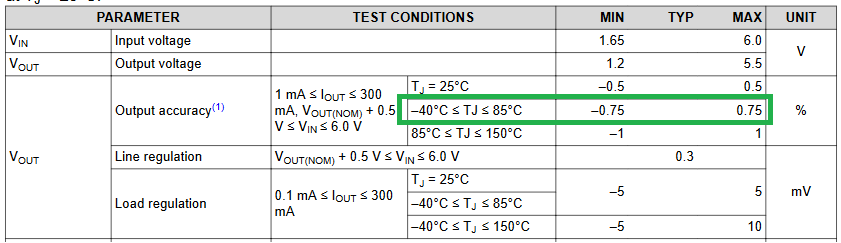
TPS784's datasheet shows a good accuracy number of 0.5% on page 6, and 1.5% on page 21. I noticed that CircuitEXP lately demonstated that TPS784 can only achieve a 5% output accuracy per their online tutorial.
It seems that, to achieve 3% accuracy, the resistance needs to be much lower for TPS784 due to the bias current variation. Could you please confirm the analysis result shown in table 8-1 in the datasheet?
Hi Derek,
It is true that worst case analysis is performed in industry, but the question comes up "what defines worst case"? Worst case analysis is different than 6 sigma or 3 sigma statistical analysis. I have used 6 sigma statistics to review the CircuitEXP answers and I can achieve similar results. So if you assume each parameter is Guassian, and you assigned 6 standard deviations to each tolerance, then you do the math, you will get similar results as CircuitEXP. Again, we have additional knobs to use in our tool which makes our simulation results more accurate than CircuitEXP. I plan on writing a white paper in the near future which builds on the paper I link in the previous response, and I hope to release the tool so that others can use it as well. You can safely assume that all parameters are guassian (Vref, resistors and bias current). Vout tolerance is guassian (I have used Crystal Ball to confirm using simulation data in the past).
The datasheet table should not be listing the design example as 1.5% tolerance, after rerunning the simulation for that example I can confirm that it will not meet the 1.5% tolerance from either a 3 sigma perspective or 6 sigma perspective. I would use the values in my reply to obtain lower tolerance setpoint resistors for this setpoint.
Your interpretation of the data is correct. 3 sigma gives -2.5% and 6 sigma gives -4.3%. There is also the positive tolerance to review. 3.274+0.0192*3, which when calculated gives 0.958% (so -2.5% / + 0.958%). For a 6 sigma design, 3.274+0.0192*6, which when calculated gives +2.7% (so -4.3% / +2.7%). When you look at this long enough, you'll realize that these tools are trying to shift the sensitivity to the reference voltage tolerance while also moving the average closer and closer to the desired Vout.
The reasoning on lowering the Vref from +/- 1.5% to +/- 0.75% comes from the electrical characteristics table. The design example stated that the temperature was 85C max. At a reduced temperature range the fluctuation on Vref is lower and the tolerance is improved.
Bias current is always a difficult parameter to work with in my experience. There are several challenges here. The measurement of such low current values is very difficult, in modern LDO's it is often 10 nA or possibly even less. Taking this measurement to confirm the device is meeting the datasheet spec can be difficult in the presence of noise at these levels. The datasheet will increase the limits to ensure that we have margin for our own manufacturing processes. For a specification like the TPS784, where you have a typical of 10nA but limits of -100nA and 50nA, the worst case scenario is the take the average (-25nA) and use a tolerance of 75nA. If you want to be conservative you assign 3 sigma to that 75nA tolerance. Or you can assign a more realistic 6 sigma, which is what I believe the CircuitEXP tool might be doing. My tool can assign different distributions to each parameter, however on review they are well modeled as Guassian so that is how I usually run the analysis.
Thanks,
- Stephen
