Hi specialists:
The document (mmwave_mcuplus_sdk_04_02_00_02\mmwave_mcuplus_sdk_04_02_00_02\ti\datapath\dpc\objectdetection\objdethwaDDMA\docs\doxygen)
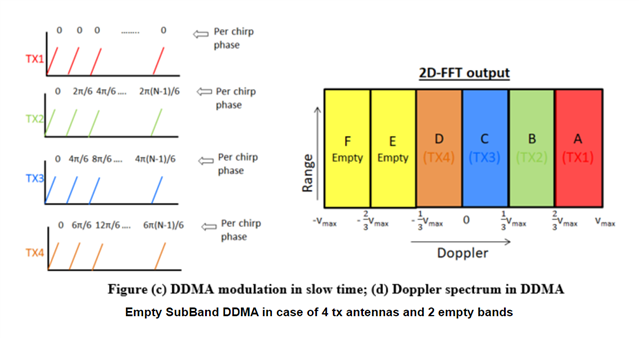
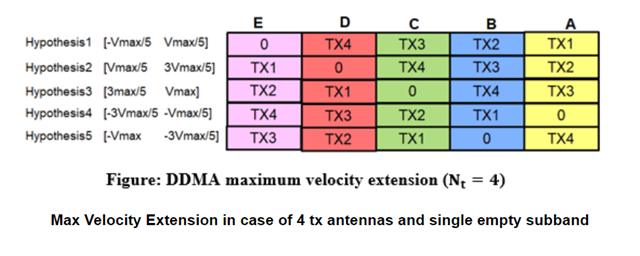
mentioned that one can recover the maximum velocity using hypothesis testing with zero padding or phase dithering for the Classical DDMA scheme.

I have questions as follows:
- How can we recover the maximum velocity using hypothesis testing with zero padding or phase dithering?
- For implementation, how does the cyclic memory shifting be applied to hypothesis test ?
- why is the single target in the same range/Doppler bin assumed?
Thanks.
Regards,
Stan