• State Resolved
  • Locked Locked
  • Replies 7 replies
  • Subscribers 30 subscribers
  • Views 1107 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

DCA1000EVM: Data processing: FFT 2D - Doppler

Tuan Trinh
Prodigy 135 points
Part Number: DCA1000EVM
Hi TI Customer Support, 
I am using AWR 1243 BOOST with DCA1000EVM capture board. I have a question.
1. I built a user app in Python programming to capture raw data from an AWR1243BOOT using a DCA1000EVM capture card. I collected successful raw data and processed 1-D FFT (Range-profile) in real-time. However, when I process FFT 2-D then have problems with the result. The figure below is the result (static environment) when I ran the app in real-time:
In a static environment, the result must be like in mmwave studio in the Figure below:
 
- Did I process FFT 2D incorrectly? Below is the MATLAB code for the FFT-2D processing I used:
function [out_dBFS] = fft_2d(adc_Data) % size adc_Data [Num. of chirp Loops ADC samples] - complex data type
Hann_win = hanning(256)';
f1 = adc_Data.*Hann_win;
fft_2 = fft2(f1);
out_fft2d = abs(fftshift(fft_2));
out_dBFS = 20*log10(out_fft2d);
end
P/S: ADC samples = 256; Num. of chirp Loops = 255. 
GrinGrinGrin

Regards,
Tuan Trinh The
  • 0
    TI__Mastermind 20605 points

    Hi Tuan,

    The fft2() directly applies a 2D FFT on your data without any intermediate pre-processing step such as windowing. You will have to perform windowing on your 1D FFT data also before performing doppler FFT on the same. This should give you a much better output.

    Thanks & regards,

    Kaushik

  • 0 in reply to Kaushik Gowda
    Prodigy 135 points

    Hi Kaushik,

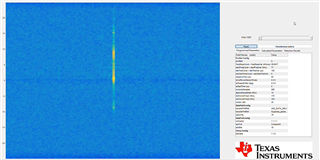
    I used MATLAB above to FFT-2D and have resulted in the Figure below:

    Amplitude is in dB (left) in mmwave studio, (right) is my result. How to convert to dB?

    I processed FFT-1D correctly.

    "You will have to perform windowing on your 1D FFT data also before performing doppler FFT on the same". Do you mean FFT 2-D base on FFT-1D?

    Regards,
    Tuan
    BlushBlushBlush
  • +1 in reply to Tuan Trinh
    TI__Mastermind 20605 points

    Hi Tuan,

    It looks like you have already converted your result to dB scale. The figure on the left has power expressed in dBFS scale, which is why you see that difference.

    To answer your second question, yes. Your code should look something like this:

    fft1D = fft(adcData.*win1D) % -> Dim 1

    fft2D = fftshift(fft(fft1D.*win2D)) %-> Dim 2

    Regards,

    Kaushik

  • 0 in reply to Kaushik Gowda
    Prodigy 135 points

    Hi Kaushik, 

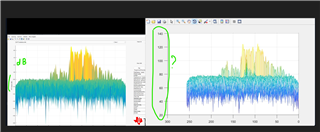
    I performed FFT2D base on FFT 1D, and the result is the same with FFT2 by fft2(). I have a question:

    The left figure result from mmwave studio, and the right figure is the result of my process. What is the noise outlier in the red circle?

    Regards,
    Tuan
    BlushBlushBlush
  • 0 in reply to Tuan Trinh
    TI__Mastermind 20605 points

    Hi Tuan,

    The observation that you are pointing to occurs when you apply a finite point FFT on a given data. The energy corresponding to the frequency of the peak bin spills over into its surrounding bins as fractional components of frequency cannot be represented on the respective bin. For example. - N point FFT on a signal sampled at Fs yields a spectrum that ranges from 0 to N which directly maps from 0 to Fs where each bin represents the energy of a particular frequency (0, Fs/N, 2Fs/N, 3Fs/N, .... Fs). If your peak frequency cannot directly map to a particular bin, the energy spills over into its neighboring bins.

    This effect can be effectively reduced by the application of a window before applying FFT. 

    Therefore, can you confirm that you have applied a window across the chirps before performing FFT across the 2nd Dimension? 

    Regards,

    Kaushik

  • 0 in reply to Kaushik Gowda
    Prodigy 135 points

    Hi Kaushik, 

    I used the Hanning window:

    1D window : multiply "hanning(num ADC sample)" function with adc data(num ADC samples)

    2D window:  multiply "hanning(num ADC sample)" function with adc data(No.of chirp loops; num ADC samples)

    Is this correct?

    Regards,
    Tuan
  • +1 in reply to Tuan Trinh
    TI__Mastermind 20605 points

    Hi Tuan,

    Please check this

    Tuan Trinh said:
    2D window:  multiply "hanning(num ADC sample)" function with adc data(No.of chirp loops; num ADC samples)

    2D window:  multiply "hanning(num chirps)" function with FFT 1D data (No.of chirp loops; num ADC samples)

    Regards,

    Kaushik