Hi,
I collected 3D point cloud data using the mmWave visualizer with one subject executing a T-pose statically indoors (see scenario below). The subject faces the radar sensor placed at 125 cm above the floor at 0 degrees to radar's boresight at all times.

Subject maintained this pose for 90 seconds without moving and during this period the 3D point cloud data has been accumulated. I then created an aggregated 3D plot where I keep all of the detected points visible on the plot. (The 3D point cloud displayed on the mmWave visualizer does not keep the points from one frame to the next, which is the key difference with my approach)
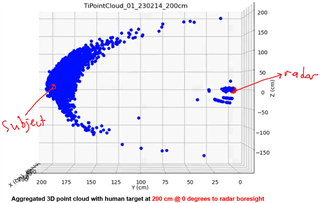
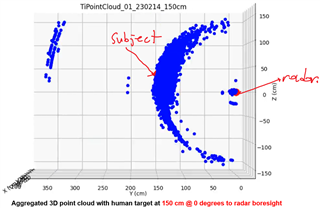
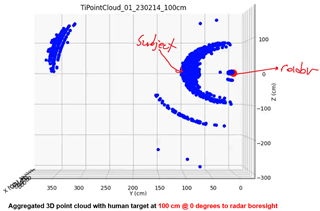
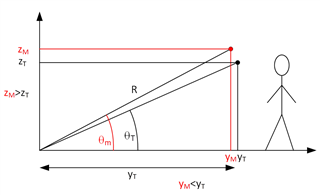
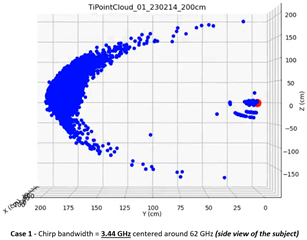
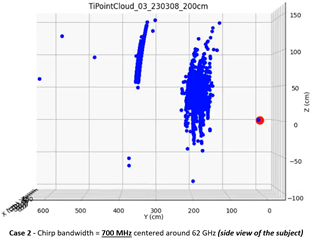
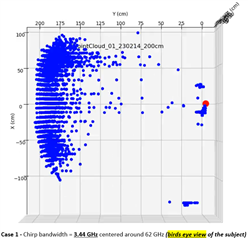
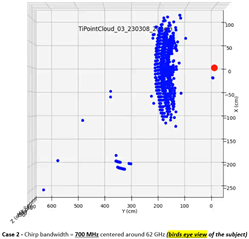
After aggregating the incoming 3D point cloud data, I generated the first 3D plot below. I annotated the radar position and the subject's detected location in red. The displayed 3D point cloud view is a representation of how the scene looks when directly looking at the subject on his right side (as indicated with the eye sketch in the photo above). As expected, I am seeing the subject at 200 cm at 0 degrees to radar boresight. (I can also see intermittent ghost objects in the vicinity of the radar, which is also expected) The density of the point cloud in the vicinity of the subject at 200 cm confirms consistent target reflections are successfully captured. However, an interesting consistency is also observed in the form of a concave shape, which I cannot understand. This shape suggests the radar is detecting the human target almost as a half spherical shape. I repeated the same experiment with the subject at 150 cm and 100 cm. The same concave/crest shape of the aggregated point cloud is still clearly visible in the generated plots (please see the last two plots below)
I would have expected the aggregated point cloud to look almost straight given the straight posture of the subject (and the expected reflections from the head and the legs). Also, a slightly convex shape of the point cloud would have made more sense compared to the concave shape I have obtained.
Can you provide insights into why I am observing this crescent shape consistently in the point clouds I generate? Do I need to apply a transformation to the point cloud for correction at all? How is one supposed to interpret this visual information?
Thank you for your help.
Regards,
Cagri