Hi team,
I'm reading our docs in mmwave L sdk and I notice such 2 questions in our mmwave demo documentation:
1. In our doc, we calculate x, y z in such ways
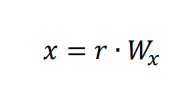
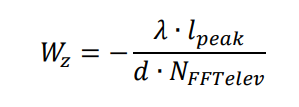
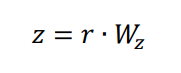
As we know, x=r*cos(Φ)*cos(θ), y=r*sin(Φ)*cos(θ), z=r*sin(θ), so, can you tell me why Wx=cos(Φ)*cos(θ) and Wz=sin(θ)?
2. In position interpolation, we use 2 formulas to calculate the bias
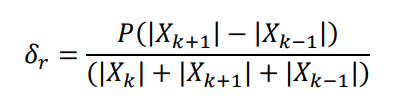
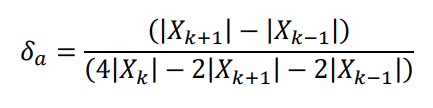
In the doc's reference, they say the formula2 is statistically biased and performs poor in noise. So why we still use it to calculate δa?
HI, there:
When the antenna is 2D array, the phase difference between two antennas is defined as below.
In order to using 2D FFT approach to implement Bartlett beamforming, we have to define sinθ cos∅ as Wx and sin∅ as Wz. And then the x, y, z can be computed as below.
For your second question, you should be able to disable the azimuth angle interpolation. Customer can disable this feature if the performance is not beneficial and implement their own interpolation algorithm.
Best,
Zigang
Hi, Shawn:
If you looked at 2D FFT definition,
you will see that you have to fit the phase change into two rotator Wm (in our case Wx), and Wn (in our case Wz). One rotator can only be indexed by j (which can be mind in our case), and other one can only be indexed by k (which can be nind in our case).
Let me know if it is helpful.
Best,
Zigang
Hello Shawn.
I attach a simple slide to make the conversion from FFT grid into the Cartesian coordinates clear:
I think the missing point in your equation is; FFT does not measure the φ and θ directly. It actually measures the μ and υ. SO a conversion is needed. Once you make this conversion according to the slide below, you will see that all the cos/sin computations are cancelled out and you will get the final value as noted in the SDK documentation.
I hope this will make it clear.
Regards.
Muhammet
