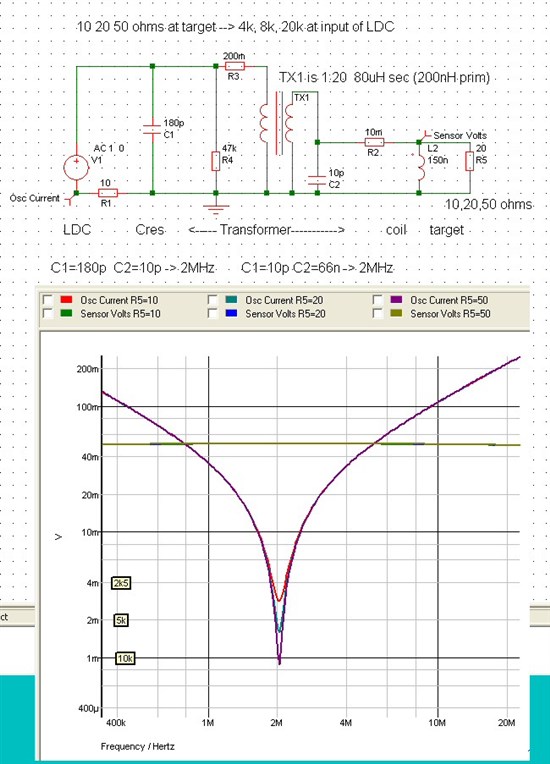
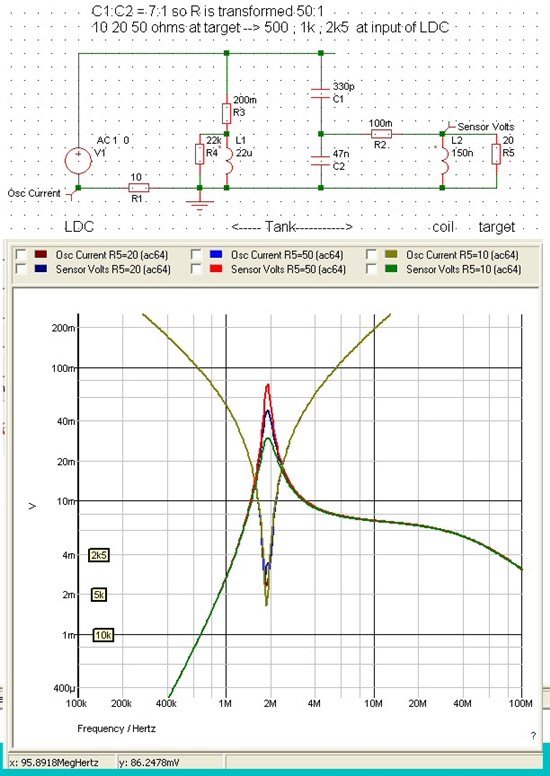
Hello all,
I’m currently evaluating LDC1000 for a coil inductance variation measurement application (we are currently waiting for the EVM shipping). I have carefully read the datasheet but I have not been able to completely understand
- the internal process used by the LDC1000 to measure inductance
- how to express the resolution on the inductance measurement
As far as I understand the datasheet the inductance measurement process necessarily uses two counters: one is connected to the oscillator and the other to the reference clock. The first one count oscillator pulsations while the second one measure the time elapsed.
First, I’m not sure about the role played by the ResponseTime register. Does it set the number of oscillator periods or the number of reference periods to count?
Secondly, I’m also wondering about the meaning of the 1/3 factor in the derivation formula. Does it means that the real counting frequency is fext * 3 for the reference counter?
Concerning the resolution, I don’t understand in what extend 24 bit announced in datasheet are defining the resolution. If the inductance measurement is based on averaging the oscillating frequency by counting the number of periods that occurs during a known time, the 24 bits only avoid counter saturation during that time. In this case the resolution on frequency measurement (and so on inductance measurement) is set by the speed at which counters operate and not by the size of the counter (I would say it is different from ADC resolution): the faster the counter are, the smaller the minimum dT the circuit can measure is. Furthermore, the resolution must also take in account the averaging process.
Many thanks for giving any precisions or opinion on that topic
Regards