Hello,
currently I am trying to define some chirp profiles and frames.
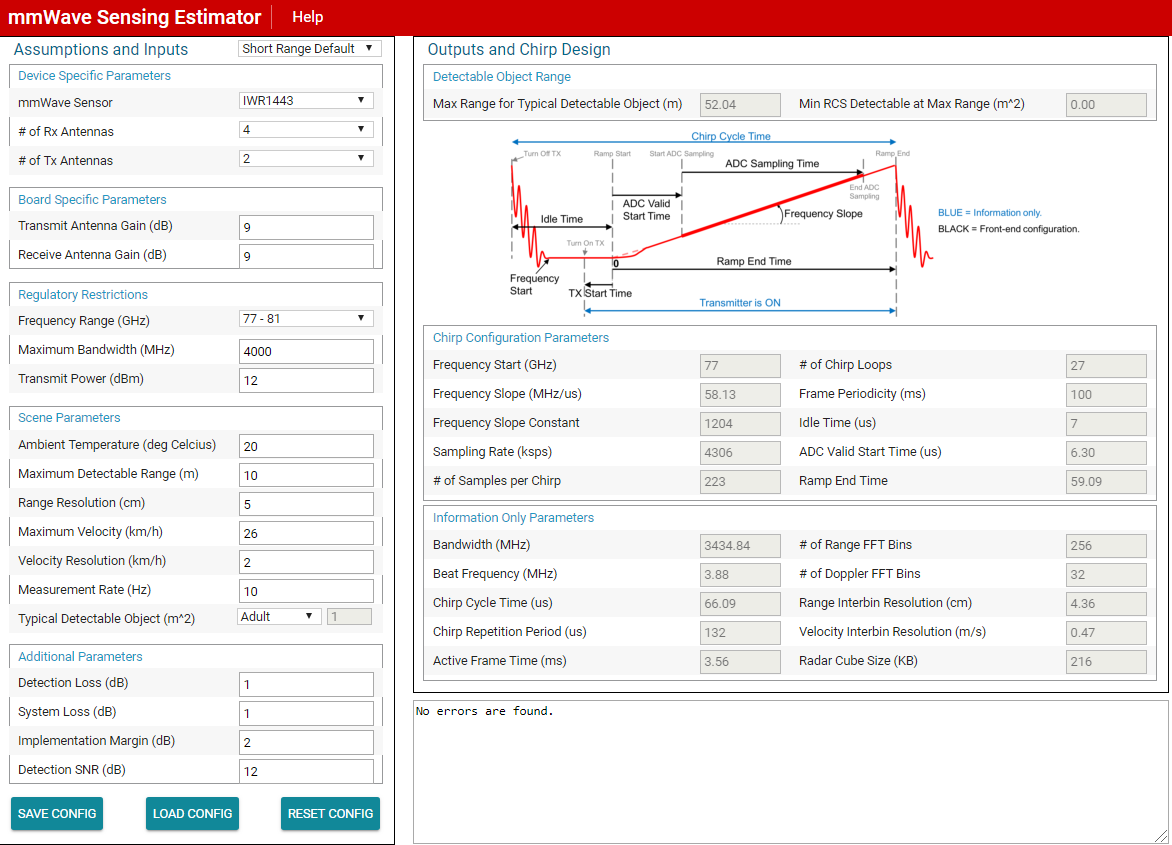
To get a first impression, I used the sensing estimator and tried to verify the calculated parameters.
I have some issues understanding the calculation for the Radar Cube Size.
For my understanding the Radar Cube Size should be calculated in the following way:
size = n_rx * n_tx * n_range_fft_bins * n_doppler_fft_bins * sampleSize
(where sampleSize is equal to 2*16 = 32 bit for complex sampling).
For the default settings (when starting the estimator) this is:
size = 4 * 2 * 256 * 32 * 32 = 2.097.152 bits
or size = 2.097.152 / 8 / 1024 = 256 KB (Kilobyte)
The size calculated by the estimator is 216 KB (see attached picture).
Where is my calculation wrong?
Thank you and best regards,
Enric