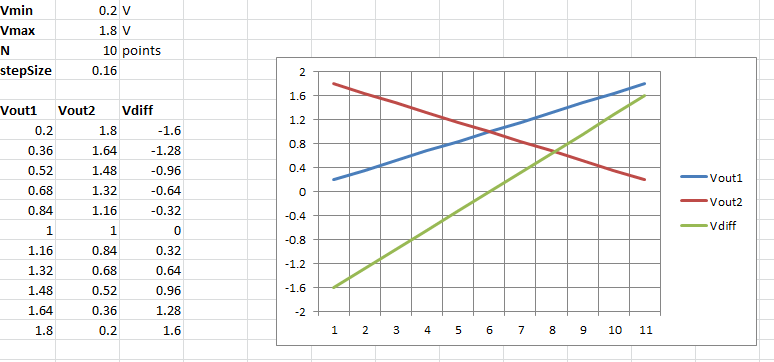
Can one increase the sensitivity by using '2' Hall-Effect sensors (DRV5053) back to back (opposing slopes of mV/mT), with '1' magnet on one side of these sensors?
I thought that Hall the Hall Voltage: Vh = Rh[I/T * B)
and hence he Hall Voltage is Inversely proportional to the thickness of the hall element. Also directly proportional to the incident Magnetic Flux density (B).
It is my understanding that the Magnetic Flux density will be reduced (by a value equal to F = qvB.
Where the Force 'F' results in a hall voltage Vh.
This Force is halved due to the fact that '2' sensors are used back to back (for a given, common magnetic field).
CAN ANYONE VERIFY the above statements?
Regards,
-Satish