• State TI Thinks Resolved
  • Locked Locked
  • Replies 6 replies
  • Answers 2 answers
  • Subscribers 30 subscribers
  • Views 1545 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

CCS/AWR1843BOOST: The computation of AOA and doppler compensation

Rata Zhang
Expert 2840 points
Part Number: AWR1843BOOST


Tool/software: Code Composer Studio

Hi，

I have three questions in the belowing:

The first question is about the computation of AOA. In the index.html of HWA  AOA DPU part, the elevation angle is calculated as follows  if Wx has been obtained:

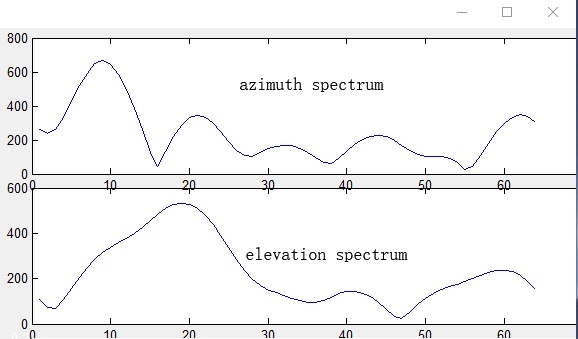
In theory, I can understand 'An FFT of the above signal will yield a peak  P2 at Wx', but the real situation is not so.I will show some  acquisition data in the bellowing:

From the figure above, we can see that the positions of the max peak point are different for the aimuth and elelvation spectrum.Doppler compensation is not done in the test, is this the reason for the  difference?

The second question  is about doppler compensation.For the radar,once the installation position is determined,the range and doppler compensation should be done,is that right? That is to say, the compensation values for differet position radar is different,  what I understand is right or not.

The final question is also with the doppler compensation.  In the mmwave_sdk_03_01_01_02 file,there is a calibration file profile_calibration.cfg,if I have done the calibration and obtain the doppler compensation values according to the configuration file, now I need to achieve greater distance, the parameters must be changed in the file,will the doppler compensation values be suitable for  the new configuration?Or I have to do doppler compensation  operation again for the new configuration?

Thanks,

Regards,

Rata

  • 0
    TI__Expert 4720 points

    Hi Rata, 

    1) Why do you expect the max peak point to be the same for both elevation and azimuth spectrum? They should be different based on the target orientation, right? 

    2) Doppler compensation is only performed in the 2 TX TDMA case (3 TX TDMA case). In such a case, each Tx is activated once every 2 (or 3 ) chirps. In such a case, it is necessary to compensate the phase of a target in the 2nd chirp (or 2nd and 3rd chirp) for the delay between it and the first chirp, in order to use combine the data from the 2 (or 3) chirps in angle processing. 

    3) The calibration doesn't have anything to do with doppler compensation. It is only concerned with angle estimation. In general, you shouldn't need to redo calibration for every change in sampling rate - since it is a fixed offset due to the antenna mismatches. 

    Regards

    Anil

  • 0 in reply to Anil Mani
    Expert 2840 points

    Hi Anil,

    Thanks for your reply,but I still have some questions as follows：    

    For the first question, I also have some doubt. According to the FFT property two sequences such as Ae^(jw0)[1,e^(jw), e^(2jw),e^(3jw),e^(4jw),e^(5jw),e^(6jw),e^(7jw)]  and  Ae^(jw0)[1,e^(jw),e^(2jw),e^(3jw)] are  performed by FFT with N points,the peak points for the two sequences should be the same,such as the 3th point. I think it is reasonable the max peak point should be the same for both elevation and azimuth spectrum.   

    For the third question,I got it. I have another question, why is doppler offset  induced by antenna mismatches?  My understanding  is that for 2 TX TDMA case as exmple，the source of modulated wave is same,,the signal of the second tx antanne has a time delay Tc for TDMA reason,  which generates phase shift δ,is that right?If not,what is the correct explanation?

    Thanks,

    Regards,

    Rata

  • 0 in reply to Rata Zhang
    TI__Expert 4720 points

    Hi Rata, 

    I finally understood your question. The two FFTs (of the 'top row' of virtual antennas, and the 'bottom row' of virtual antennas) should be the same. The fact that they aren't implies that there is some mismatch between the antennas - Have you done a zero-angle calibration? 

    Regarding your next question - 'doppler offset does not induce antenna mismatches'.

    The received signal corresponding to the 2nd Tx  (called '2nd Tx Signal') is exactly the same as the received signal corresponding to the 1st Tx (called '1st Tx Signal) if the target is at bore-sight and at zero relative velocity. If the target is not at boresight then we can expect a phase difference corresponding to the angle.

    If the target is not at zero-velocity, we expect an additional phase difference (because of two facts - that the target has non-zero velocity, and that the two signals have a time-offset between them) - this phase difference is removed in doppler compensation. 


    Regarsd

    Anil

  • 0 in reply to Anil Mani
    Expert 2840 points

    Hi Anil,

        Thanks for your reply,but I still have some doubts.

        For the first question,my understanding is as follows: If I do zero-angle calibration,the two spectrums should be the same, is that right? I have another question, I consider that zero-angle calibration  means Range Bias and Rx Channel Gain/Phase Measurement and Compensation, is it right?

        For the next question,I mix doppler compensation and Range Bias and Rx Channel Gain/Phase Compensation,I thought they were the same before. Now I understand that the bias in the receive channel gain and phase is introduced by antenna layouts on the board and RF delays in SOC, and is fixed. While the doppler bias is induced by non-zero velocity and a time-offset between the two signals as you said.

       Finally, I still have a question,why is Rx channel gain/phase compensation done after 2D FFT?I am looking forward for your reply.

      Regards,

      Rata

  • 0 in reply to Rata Zhang
    TI__Expert 4720 points

    Hi Rata. 

    Yes, zero-angle calibration means 'Rx Channel Gain/Phase Measurement and Compensation'. 

    Regarding, why 'Rx channel gain/phase compensation' done after 2D FFT - the answer is better SNR (because of 2D-FFT). 

    Regards

    Anil 

  • 0 in reply to Anil Mani
    Expert 2840 points

    Hi Anil,

      Thanks for your reply.I still have two question.The first one is why the SNR is better after 2D-FFT. The other one is Why the RX channel gain/ phase can be compensated by doing so?

    Thanks,

    Regards,

    Rata