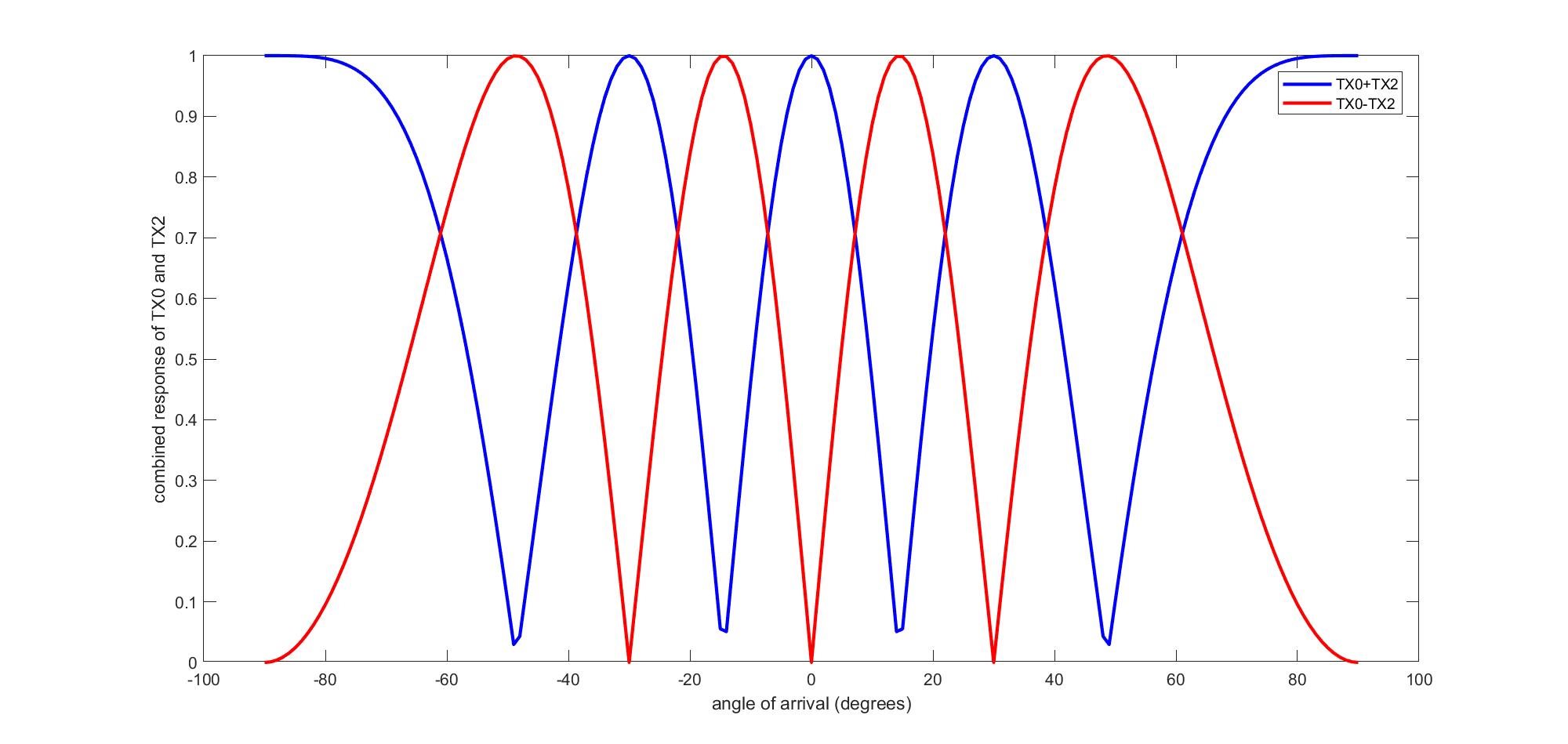
Hi TI,
Do you have any diagrams of TX antennas (e.g. TX0 and TX2) in first and second iteration of BPM (when transmitting both at once)? I can imagine the first case where TX0 and TX2 phases are equal.
However, I'm curious about opposite phases of transmitted signal as it could results in something like extreme case of beamforming.
Thank you for your answer, Lukas
Hi Lukas,
A different way to understand this is to think of BPM as a super-position of the TDM use-case.
Consider a single RX antenna that is listening to the transmissions from TX0 and TX2.
1. When TX0 is transmitting, let the received signal be S1.
2. When TX2 is transmitting, let the receive signal be S2. Likewise if TX2 is transmitting with a 180 degrees phase , the received signal would be -S2
By super-position (the EM waves add linearly), the received signal when both TX0 and TX1 are transmitting in phase will be Sa= S1+S2 (just the sum of the individual transmissions). Likewise when TX0 is transmitting as is, and TX2 has a 180 degrees phase imparted - the received signal will be Sb-S1-S2.
Thus with knowledge of Sa and Sb, the signals S1 and S2 can be calculated. Note that : in this description I ignore the object velocity, otherwise there is a velocity induced phase correction required.
BTW, I am attaching a plot of the combined antenna response (TX0+TX2, TX0-TX2), when TX0 and TX2 are 2*lambda apart (as in the 6843 ISK). You can see that the two responses nicely complement each other (one has peaks , in places where the other has nulls)
Sandeep
