Other Parts Discussed in Thread: AWR1443, AWR1243,
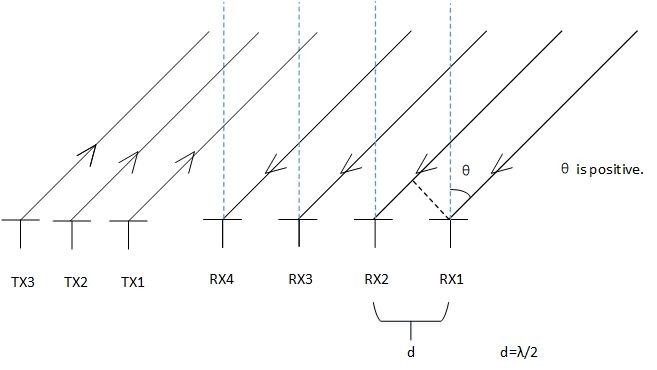
According to some documents of TI, the receiving antennas of AWR1443 are arranged as follows.
Fig. 1
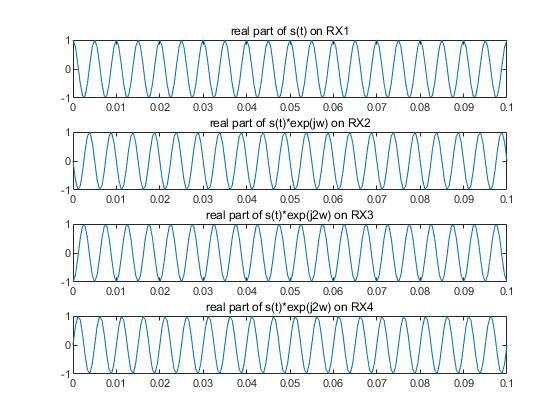
If we assume the expression of the signal at RX1 is s(t), because the signal at other antenna is a delayed version of s(t), then the signal at RX2, RX3, RX4 can be expressed as s(t)*exp(-j*pi*sinθ), s(t)*exp(-j*2*pi*sinθ), s(t)*exp(-j*3*pi*sinθ) respectively. Then, an angle-FFT on these signals corresponding to different RX antennas will generate a peak at ω=-pi*sinθ, which means that the angle estimated by angle-FFT is negative. In other words, if the target is on the right of the arrays, the angle is negative.
However, in our experiments, when the target is on the right of the antenna arrays, we can obtain a Range-Angle-Map as follows.
Fig. 2
From the picture we can see that, when the target is on the right of radar, the angle estimated by angle-FFT is positive, but this result is contradictory to our analysis.
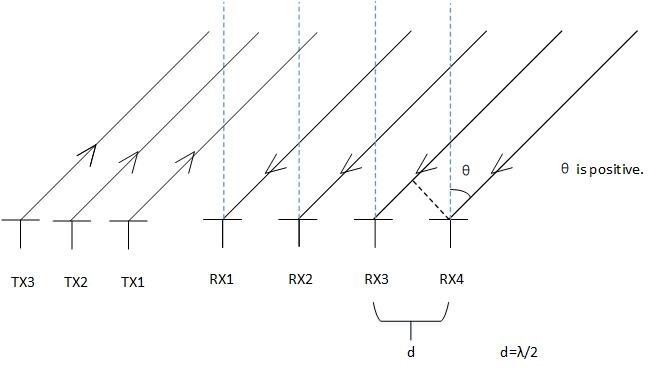
However, if the receiving antennas were arranged as follows, the experiment result would be consistent with the analysis.
Fig. 3
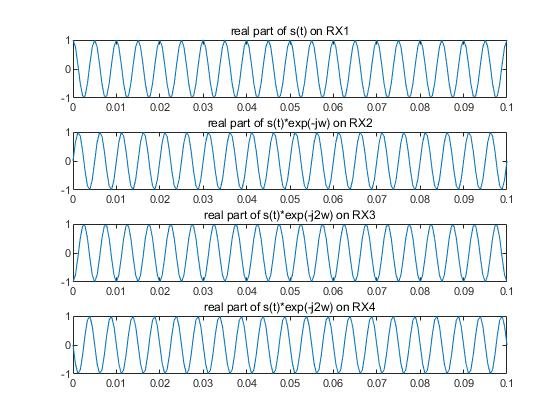
In Fig.3, the signals received by RX1, RX2, RX3 and RX4 can be expressed as s(t), s(t)*exp(j*pi*sinθ), s(t)*exp(j*2*pi*sinθ), s(t)*exp(j*3*pi*sinθ) respectively. Then an angle-FFT on these signals will generate a peak at ω=pi*sinθ and this means that the angle estimated by angle-FFT is positive. What’s more, this analysis is consistent with our experiment result.
So I think the antenna arrangement shown in Fig. 3 is correct and there may be some errors in some documents, but I’m not sure I’m right. So I want to know whether my analysis is correct, thank you.