This technical article was updated on July 23, 2020.
In my previous blog post, I explained a simple serial interface in which each data bit is transferred as it is resolved. I also noted that this type of interface is usually restricted to lower resolution or lower speed register (SAR) analog-to-digital converters (ADC).
Most of the modern, high-resolution (>12 bits) SAR ADCs employ redundancy and error-correction techniques to improve the performance of the ADC, especially at higher throughput rates. In such ADCs, the final conversion result is available only after the entire conversion process is complete.
Interface type 2: Data bits are transferred as soon as the conversion process is completed
This type of SAR ADC completes the conversion process for sample S and then transfers the conversion result to the host controller while it is acquiring the next sample, S+1. The host controller issues the Start-Of-Conversion (SOC) for sample S+1 only after receiving the conversion result for sample S.
The data transfer between the ADC and the host can be parallel or serial.
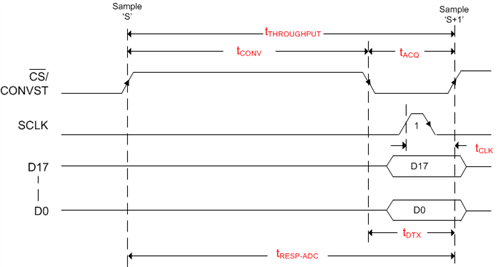
Figure 1 shows an example parallel interface.
Figure 1: Parallel Interface
For parallel data transfer:
- tDTX = tCLK
- tRESP-ADC = tCONV + tCLK
- tTHROUGHPUT = tCONV + tACQ
- tRESP-ADC ≤ tTHROUGHPUT
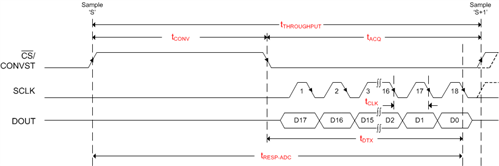
Figure 2 shows a simplified version of the serial interface implemented in the ADS8881:
Figure 2: Simplified Type 2 serial interface used in ADS8881
For serial data transfer:
- tDTX = n*tCLK
- tRESP-ADC = tCONV +n* tCLK
- tTHROUGHPUT = tCONV + tACQ (as long as n*tCLK < tACQ – i.e., for faster clock speeds)
- tTHROUGHPUT = tCONV + n* tCLK (as long as n*tCLK < tACQ – i.e., for slower clock speeds)
- tRESP-ADC ≤ tTHROUGHPUT
In a typical control system application using the ADS8881, the host controller will:
- Issue the start-of-conversion (CONVST) signal and wait for the conversion to complete.
- Initiate a serial data-transfer frame and receive the conversion output data for sample S.
- Sample S+1 starts being acquired while sample S was being readout.
- Take a control action based on the data received from sample S.
- Issue the next start-of-conversion signal to see the effect of the control action in sample S+1.
As shown in the equations, SAR ADCs employing a Type 2 interface scheme will have a restriction of minimum clock speed to achieve the desired throughput.
- tCLK < (tTHROUGHPUT - tCONV)/n
Let’s use the ADS8881 as an example:
- tTHROUHGPUT = 1 µs, tCONV = 710 ns and n = 18
- tCLK < (1,000 – 710)/18 < 16.1ns (i.e., fCLK > 62 MHz) to achieve 1 Msps throughput
For slower clock speeds, the response time AND the throughput will become slower:
- With fCLK of 62 MHz, tRESP-ADC = tTHROUGHPUT = 1 µs
- For fCLK of 26 MHz, tRESP-ADC = tTHROUGHPUT = 1.4 µs
- For fCLK of 16 MHz, tRESP-ADC = tTHROUGHPUT = 1.84 µs
In the next installment of this series, we’ll look at another type of serial interface that will allow the SAR ADC to maintain high throughput even at lower clock speeds. Which parameter do you think will degrade?
Additional resources:
See a SAR ADC applied in five TI Designs reference designs, optimized for various industrial data acquisition applications.
Read a post by my colleague Harsha Munikoti on how SPICE simulation tools for SAR ADCs can provide accurate and painless computer-based performance estimations.
See additional posts in the SAR ADC Response Times series.
Visit the precision data converters forum on the TI E2E Community to learn tips, tricks and techniques from TI precision analog experts.

-

Minori Hanashima
-
Cancel
-
Vote Up
0
Vote Down
-
-
Sign in to reply
-
More
-
Cancel
Comment-

Minori Hanashima
-
Cancel
-
Vote Up
0
Vote Down
-
-
Sign in to reply
-
More
-
Cancel
Children