Hi,
looking for documents on opamp stability and TINA TI modeling, I have found a good article by Tim Green (part 2 of his series about stability) but I have some points that I would like to clarify to me.
In the article, a simple TINA model of OPA364 is derived from the datasheet.
The first method, quite approximate, places the first pole fp0 at 29Hz (where phase is -45°) and the second pole fp1 at 25 MHz (where phase is -135°).
The second method, that leads to more accurate results, adds instead a triple pole at 200MHz (fp3).
Here are my doubts:
1) The -45°/dec slopes depicted in fig 2.17 seem to be too steep. They make almost a 60° step in one decade (not 45°).
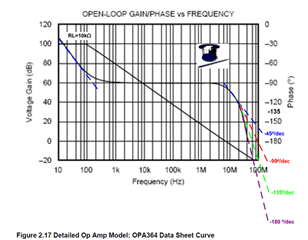
2) In the second method, the previously found fp1 frequency (25MHz) is kept valid despite the triple pole fp3 is added at 200MHz.
But if it were the case, I should have phase influenced by the triple pole starting from 20MHz. So the -135° value, that lies at 25MHz, should be already affected fp3, because phase is decreasing more rapidly than fp1 alone. In other words, the -135° value is not longer related to fp1 pole only .
So, why not determine fp1 finding when phase starts changing (respect the -90° value) and place fp1 one decade after? In other words, with asymptotic phase graphs in mind, I could:
- draw a segment that is 1 decade width and inclined by -45°/dec (see the red segment in image below)
- place it tangent to phase diagram, with one end at the -90° value
- read the frequency of fp1 pole at the other end
This would lead to fp1 at 60MHz in this case.
Is this correct?

Thank you and regards,
Massimo Luchi

