- Ask a related questionWhat is a related question?A related question is a question created from another question. When the related question is created, it will be automatically linked to the original question.
This thread has been locked.
If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.
Hi, team!
I want to calculate ADC823+ Amp8689 error.
offset voltage error:

INA823: G=1, V(OS_RTI)=V_OSI+V_OSO∕G=(20+140∕1)uV=160.06uV V(OS_INA)=G*V(OS_RTI)=160.06uV
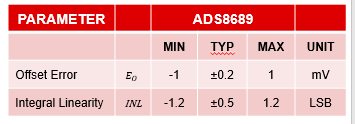
ADS8689: V(OS_ADC)=Eo=±0.2mV
V_OST=√((V(OS_INA))^2+(V(OS_ADC))^2 )≈256.16uV
Gain Error:
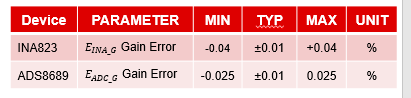
E_G=√((E(INA_G))^2+(E(ADC_G)^2+(E_R1)^2 ) R1 is sample resistor(50ohm,0.1% )
= √(0.01^2*2+0.1^2)
≈0.101%
Noise:
INA823: En_ina=√((e(nr ) )^2+(e(ni ) )^2+(e_nv ) )^2 )≈153.48uV(Resistor Noise/Current Noise/Voltage Noise)
ADS8689: V(FSR_rms)=0.5∙FSR∙0.707≈7239.68mV
E(n_adc)=V(FSR_rms)/(10^(SNR/20)) =7239.68mV/(10^(91.5dB/20)) ≈192.63uV
E(n_total)=√((E(n_ina))^2+(E_(n_adc))^2 )≈246.30uV
I want to know if there is something wrong in the above formula?
And I want to calculate total error(Etotal) ,including offset error, gain error and noise error.
Can I calculate like this?
E_total=√((V_OST/Vin )^2+E_G^2+(E(n_total)/Vin )^2 )=???
Is this formula right? And Vin is -10V~+10V, so I choose 2.5Vref as shown in figure.

E_total=√((V_OST/Vin )^2+E_G^2+(E(n_total)/Vin )^2 )=√((256.16uV/10V)^2+0.101%^2+(246.30uV/10)^2)=???%
I think there is something wrong and it's too small. Could you tell me which formula is wrong? Or provide me some document about this calculation(error about amp+adc).
Thank you so much!
Hale,
You do not specified what is the full-scale ADS range. Your calculations above were done for typical bipolar case at 25 deg C but for the worst case error analysis, you must used maximum offsets and gain limits specified in the datasheets and not typical you used.
Thus,
offset voltage error:
INA823: G=1, V(OS_RTI)=V_OSI+V_OSO∕G=(+/-100+/-450∕1)uV=+/-550uV
ADS8689: V(OS_ADC)=Eo=±1.0mV;
Also, for worse-case you must assume they add linearly and not as vector quantities.
V_OST=V(OS_INA)+V(OS_ADC)≈+/-1.55mV
You must also include differential and integral nonlinearity - see below.
Gain Error:
worst-case E_G=E(INA_G)+(E(ADC_G)+(E_R1) = 0.04%+.025%+0.1% = 0.165% (is R1 a shunt resistor? Please show schematic)
Noise:
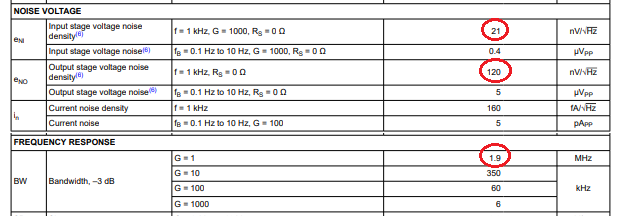
INA823: En_ina=[√((e(ni)^2+(e_no)^2 )]*√(BWn)=√(21^2+120^2)*√(1.9e6*1.57) = 122nV/√(Hz)*√(2.98MHz) = 211uVrms
You also need to include the differential and integral nonlinearity - see below.

Hi Tan,
You may also find the following TI Precision Labs Sessions useful. They discuss error calculation of amplifiers +ADCs:
Thank you and Regards,
Luis
Hi, Marek!
Thanks for your reply. I want to ask if I need to calculate ADC noise in this case and the formula is shown.
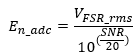
When calculating INL/DNL/Eg/Eo, is ADC noise included?
Hi Tan,
ADC noise is not included and need to be added using above formula - INL, DNL, Eg and Eo are all DC parameters and do not include the ADC noise.
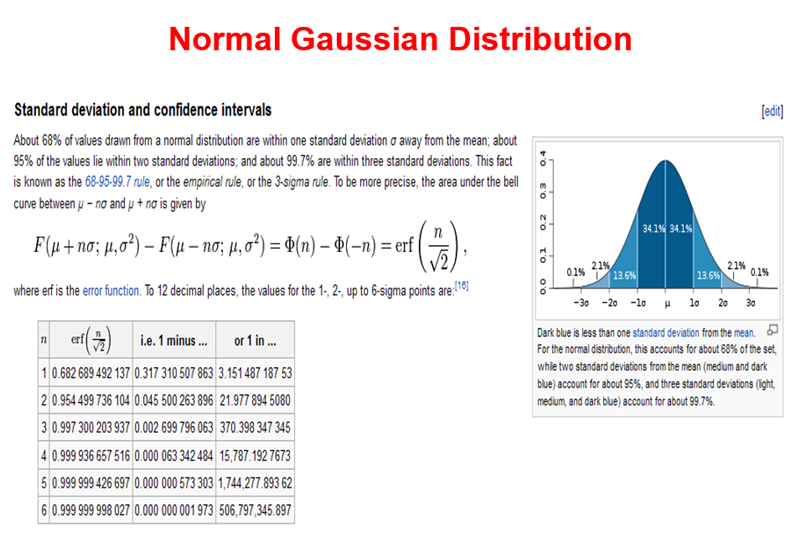
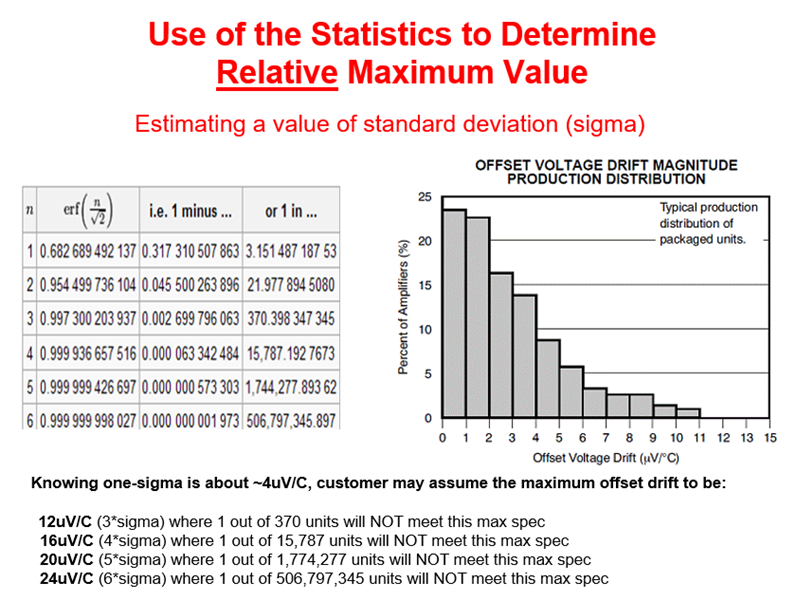
Having said that, as discussed in https://training.ti.com/ti-precision-labs-adcs-statistics-behind-error-analysis?context=1139747-1140267-1128375-1139104-1128656 the worst case analysis must be done by linearly adding maximum values of all error components (a very conservative approach) or you may use a vector addition of all typical values (1-sigma) and then multiplying the result by acceptable failure rate (number of sigmas) - see example below.