Other Parts Discussed in Thread: OPA627
Hi team,
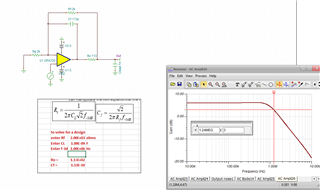
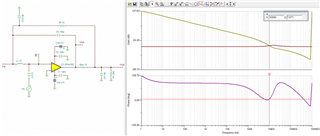
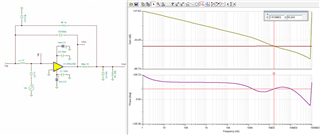
While going through oure precision video Stability- isolator resistor, the dual feedback is introduced as following:
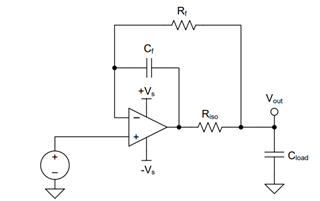
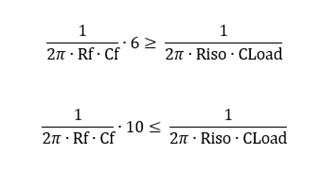
And the design steps are ad below, could you pls help to expalin a little more that how the Cf value formula comes from?

Thanks
Best regards
Mia Ma