Other Parts Discussed in Thread: OPA392, INA592, OPA2392, OPA388
Tool/software:
Dear All,
I am designing a fully differential first order low pass filter as part of an ADC drive signal chain. I want to use the THP210 and have my low pass 3db cut at ~2khz.
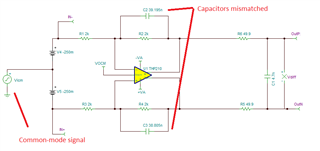
Design is as below (thanks to EDN for the sketch!)
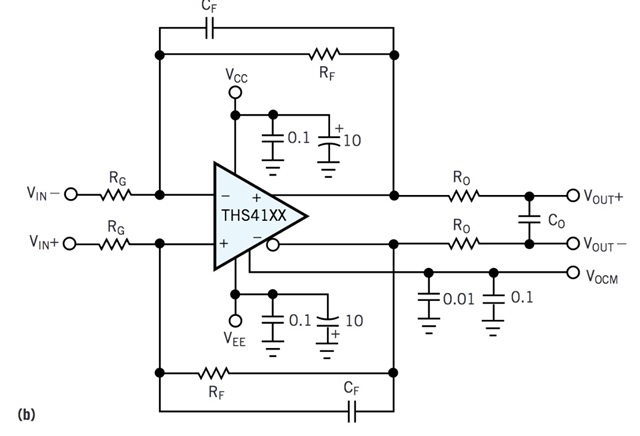
I have VCC=5V, VEE=0, VCM=2.5V.
RG=RF=2k (using a Vishay Dale 4 resistor array with 0.01% matching ratios)
Cf=39nF NP0 1% tolerance.
R0=49.9 and C0=4.7n.
After R0 is ADC differential.
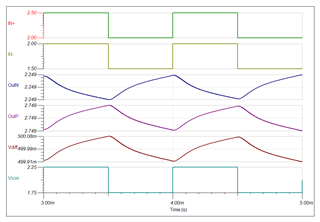
Finally, my input signals are offset square waves (in-phase) on both input pins, with the square wave frequency 1khz.
I.e. for 500us I would have VIn+=2V and VIn-=1.5V, then for 500us I would have VIn+=2.5V and VIn-=2V, and repeat. Obviously I want my output signal to be the difference between the two signals (i.e. in this case one output should be at VCM+0.5/2=2.75 and the other at VCM-0.5/2=2.25V. The overal purpose of my circuit is to measure changes in this difference (which are very slow, <10hz). I will run a SINC filter on the ADC with a frequency cut around 20hz (i.e. rather than doing more aggressive low pass filtering in this analog input part, as my impression was it would require large resistor values that would add significant noise to my signal...).
Now to my question; I believe I am doing the right thing in my calculation of Cf to give the 2khz low pass, however, does adding this capacitor also dramatically mess with the CMRR of the design - which in this case would lead to 1khz transients turning up in my outputs? If yes, my impression was it wouldnt necessarily matter because differential ADCs are typically giving >>100db CMRR - or is this a datasheet "truth" and in practice my circuit will suffer due to this extra noise injection?
I recognise this is potentially a trivial question but could not find a particularly nice explanation anywhere online...
Many thanks for advice.