Tool/software:
Hi,
This question is related to following thread.
INA849: Documentation for noise caluculation - Amplifiers forum - Amplifiers - TI E2E support forums
Carolina-san mentioned that it is difficult to show maximum noise specification for INA849.
However, I would like you to confirm whether you can confirm about below or not.
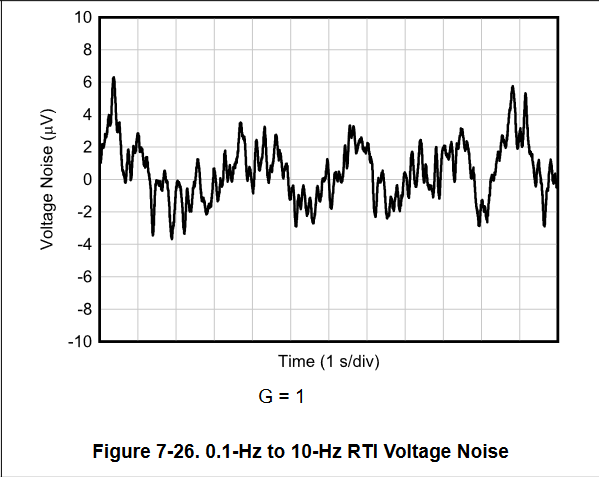
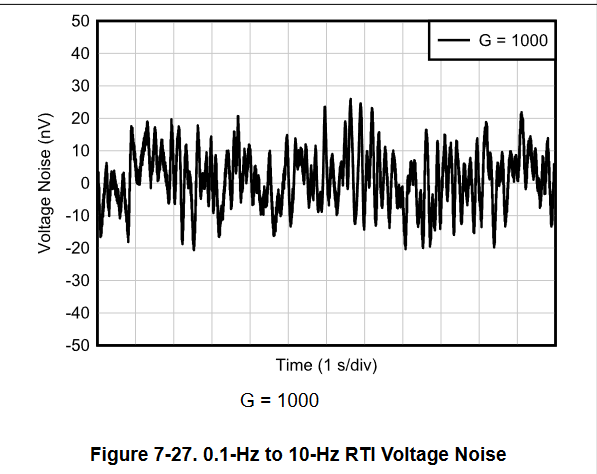
* INA849 can meet "0.2uVpp @0.1Hz - 10Hz" as RTI.
Best Regards,