Hi everybody,
I'm a newbie in electronic; right now, I’m trying to understand how to use an OpAmp to have a multiple feedback, second order band pass filter.
For what I know, 2 different solutions are possible:
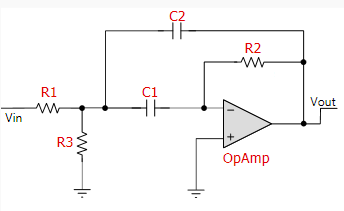
The first one (used by FilterPro) is the classic one:
The second one hasn’t the resistor “R3”:
Using this configuration, the gain of the circuit will always be equal to -2Q2.
To make this easier for you to answer, I'll number my questions.
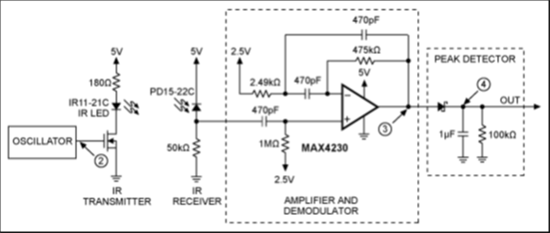
1) The configuration without “R3” is used in this document:
http://www.maximintegrated.com/en/app-notes/index.mvp/id/4622
This is the schematic:
It is an IR proximity sensor, working at a frequency of 10kHz. As you can see, the signal in feeding the non inverting input (after passing through a passive high pass filter); the inverting input is connected to Virtual Ground (2.5V).
The Op Amp used here (MAX4230) has a 10MHz Gain-Bandwidth.
Knowing that:
Fr = 1 / (2π * [√ R1 R2 C1 C2])
Q = 0,5 * (√R2/R1)
G = -2Q2.
Passband BW = Fr / Q
I have:
Fr = 9846 Hz (close to 10kHz found in the text)
Q = 6.91
G = 95.38 (close to “100” found in the text).
Passband BW = 1.4249kHz
I used theese data with FilterPro, and I had exactly the same schematic (except for “R3” 157MΩ, of course):
But you can see that the Min GBW required in really, really high: 648MHz!!!
The formula used by FilterPro to calculate it is: 100 * Fc * Gain * Q.
In “Op Amps for everyone” (Ron Mancini, pag. 337) I’ve found another formula, for second order filters with a Q greater than 1:
Considered that I selected “Butterworth” as Filter Response, I can suppose to have an “ai” of 1.414.
Using this formula, I have a Min GBW reqd. of 66MHz, which is much lower than the one calculated by FilterPro, but still higher than 10MHz (MAX4230 Gain-Bandwidth): am I missing something?
2) I read many positive comments about decompensated Op Amps. But, reading “Op Amp Applications Handbook” (Walt Jung), pag. 69, I read that: “unlike their fully compensated op amp relatives, a decompensated op amp can never be used with direct capacitive feedback from output to inverting input.”
Provided that the Gain will be adeguate (as required for the decompensated Op Amp), can I use a decompensated Op Amp for a multiple feedback, band pass filter?
3) I’m planning to use SMD capacitors with 1% tolerance; I’d like to use SMD resistors with 0,5% tolerance, but they are not readily available. Is there a big difference in using SMD resistors with 1% tolerance?
Considering that I have to use 3 resistors, is it a problem if I use 1 (or 2) resistors with 0,5% tolerance, and the missing ones with 1% tolerance? Am I going to obtain a performance beetwen the one with only 1% resistors and the one with only 0,5% resistors?
4) Using FilterPro, I see that when I get a Q higher than 15 (as always: multiple feedback, second order band pass filter) I have an asterisk close to the Q value (like: 16*). I guess it means that I’m asking too much, so is it correct to say that, until I don’t have that sign (so, until the value of Q is < 15) the circuit is expected to work properly?
Regards,
Marco