Other Parts Discussed in Thread: LMK61E2, LMX2571
Hi,
I am building a scope with the ADS 4225 and based on the fact that the max sampling rate is not 1GS/s but 125MS/s i was searching for a way to take full advantage of its' 550MHz BW.
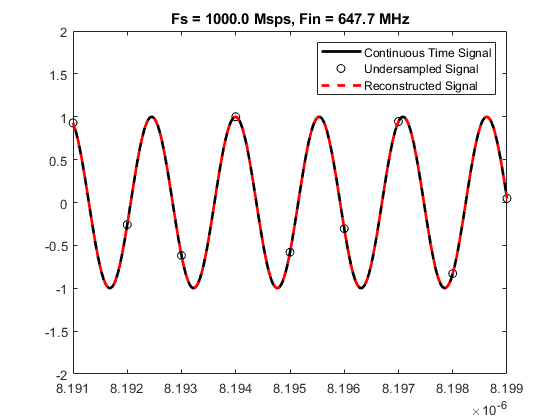
One way to do that is to use undersampling (for repetitive signals). Given that the resolution of the ADC is 12bits i need an extremely low jitter clock source.
In order to do undersampling i have to accurately measure the frequency of the input signal and then generate a precise clock frequency that will sample the input signal in just the right time.
Example:
Input signal: 70MHz (2nd Nyquist zone)
I need a sampling frequency of 1/70MHZ + 1/100 of the 70MHz period which is : 14.285nS + (14.285/100) = 14.42785nS = 69.31MHz in order to take 100 samples across 100 adjacent periods.
In order to generate that frequency i need to have a low jitter clock and then a pll which will programatically generate the sampling frequency that i need and eventually drive the ADC with that frequency.
I have chosen the clock LMK61E2 and considering the pll LMX2571.
Questions:
Is my undersampling approach correct as far as the sampling frequency is concerned?
How much will the pll output be affected jitter-noise-wise?
Any other suggestions?
Thanks in advance
Manos Tsachalidis