Other Parts Discussed in Thread: ADS112C04
Hello,
I want to implement a circuit to measure temperature using a 2-wire PT100 RTD (temp. coefficient 0.385 Ohm/°C).
The RTD element is positioned very close to the rest of the circuit, about 15 cm.
The goal is to measure temperature in the range (10°C : 50°C) with a resolution of 1°C, minimizing the hardware cost.
I know that the best approach would be to bias the RTD with precise current generator, but since the required temperature resoution is not so precise I was thinking of using a simple Wheatstone bridge circuit followed by ADS1014 ADC.
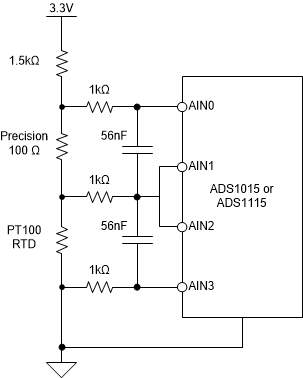
I attach the sketch of the circuit.
For the given temperature range and circuit elements I made these calculations:
- RTD range (103.85 Ohm : 119.25 Ohm)
- Vdiff range (2.4 mV : 12 mV)
- Vcm 65 mV
I would set the ADC's FSR to be +-256mV, so LSB= 0.125mV which corresponds to about 0.5°C; the full Vdiff range would cover about 80 ADC levels.
My questions are the following:
1) The common mode voltage is close to ground: is this a problem for the ADC?
2) I drew a low pass filter between the bridge and the ADC input, with the purpose of avoiding aliasing. Is this filtering approach correct? How should I size the components Ra, Rb, Cdiff, Ccm?
3) Is this circuit able to guarantee a temperature resolution of 1°C?
Thanks,
Riccardo